A cell supplies a current of 0.9 A through a $1 Ω$ resistor and a current of 0.3 A through a $2 Ω$ resistor. Calculate the internal resistance of the cell. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

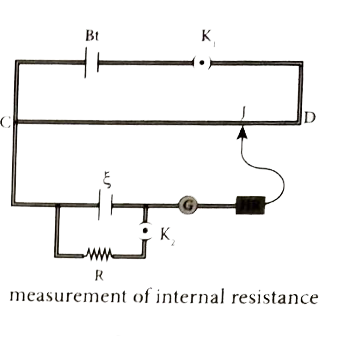
(i) Measurement of internal resistance of a cell by potentiometer: To measure the internal resistance of a cell, the circuit connections are made as shown in figure. The end of the potentiometer wire is connected to the positive terminal of the battery Bt and the negative terminal of the battery is connected to the end D through a key $K_{1}$ This forms the primary circuit.
The positive terminal of the cell $ξ$ whose internal resistance is to be determined is also connected to the end of the wire. The negative terminal of the cell $ξ$ is connected to a jockey through a galvanometer and a high resistance. A resistance box R and key $K_{2}$ are connected across the cell $ξ$ . With $K_{2}$ open, the balancing point J is obtained and the balancing length $C J = l_{1}$ , is measured. Since the cell is in open circuit, its emf is
$ξ \propto l_{1}$ ...(1)
A suitable resistance (say, 10 $Ω$ ) is included in the resistance box and key $K_{2}$ is closed. Let R be the internal resistance of the cell. The current passing through the cell and the resistance R is given by
$I = \frac{ξ}{R + r}$
The potential difference across R is $V = \frac{ξ R}{R + r}$
When this potential difference is balanced on the potentiometer wire, let $l_{2}$ be the balancing length.
Then $\frac{ξ R}{R + r} \propto l_{2}$ ...(2)
From equations (1) and (2)
$\frac{R + r}{R} = \frac{l_{1}}{l_{2}}$ ..(3)
$1 + \frac{r}{R} = \frac{l_{1}}{l_{2}}, r = R [\frac{l_{1}}{l_{2}} - 1]$
$∴ r = R (\frac{l_{1} - l_{2}}{l_{2}})$ ...(4)
Substituting the values of the R, $l_{1}$ and $l_{2}$ the internal resistance of the cell is determined. The experiment can be repeated for different values of R. It is found that the internal resistance of the cell is not constant but increases with increase of external resistance connected across its terminals.
(ii) Current from the cell 1, $l_{1}$ =0.9 A and Resistor , $R_{1} = 1 Ω$
Current from the cell 2, $l_{2}$ =0.3 A and Resistor , $R_{2} = 2 Ω$
Current in the circuit , $I_{1} = \frac{ξ}{r + R_{1}}$
$ξ = I_{1} r + I_{1} R_{1}$ …(1)
Current in the circuit , $I_{2} = \frac{ξ}{r + R_{2}}$
$ξ = I_{2} r + I_{2} R_{2}$ ....(2)
From equation (1) and (2),
$r = \frac{I_{2} R_{2} - I_{1} R_{1}}{I_{1} - I_{2}} = \frac{(0.3 \times 2) - (0.9 \times 1)}{0.9 - 0.3} = \frac{0.6 - 0.9}{0.6}$
Magnitude of internal resistance $r = 0.5 Ω$ .

Updated on:21/07/2023

|

Class 12 PHYSICS SAMPLE PAPER-1 (SOLVED)

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER-1 (SOLVED)-Questions

Home
Ask Doubt
Profile