Deduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

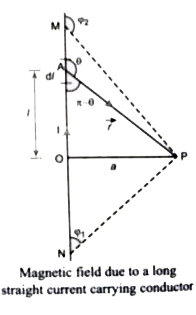
Magnetic field due to long straight conductor carrying current:Conside a long straight in wire NM with current I flowing from N to M.Let P be the point at a distance a from point O.Consider an element of length dl of the wire at a distance l from point O and $¯ r$ be the vector joining the element dl with the point P.Let $θ$ be the angle between $¯ ¯ ¯ d l$ and $¯ r$ ,Then ,the magneti field at P due to the elements is
$d ¯ ¯ ¯ B = \frac{μ_{0} I d ¯ l}{4 π r^{2}} sin θ (unit vector perpendicular to d ¯ l and ¯ r)$
The direction of the fie1ld is perpendicular to the1 plane of the paper and going into it.This can be determined by taking the1 cross product betw1e1e1n to ve1cors $d ¯$ and $¯ r$ (Let it be $\cap n$ ).The net magnetic field can be determined by intergrating with proper limits.
$¯ ¯ ¯ B = \int d ¯ ¯ ¯ B$
From the figure,ina right angle triangle PAO, $tan (π - θ) = \frac{a}{l}$
$l = - \frac{a}{tan θ} (sin tan (π - θ) = - tan θ) \Rightarrow \frac{1}{tan θ} = cot θ$
$l = - a cot θ and r = a cos e c θ$
Differentiating,
$d l = a cos e c^{2} θ d θ$
$d ¯ ¯ ¯ B = \frac{μ_{9} I (a cos e c^{2} θ d θ)}{4 π {(a cos e c θ)}^{2}} sin θ d θ ˆ n = \frac{μ_{0} I (a cos e c^{2} θ d θ)}{4 π a^{2} cos e c^{2} θ} sin θ d θ ˆ n$
$d ¯ ¯ ¯ B = \frac{μ_{0} I}{4 π a} sin θ d θ ˆ n$
This is the magetic field at a point P due to the current in small elemental length.Note that we have expressed the magnetic field OP in terms of angular coordinate i.e $θ$ .Therefore,the net magnetic field at the point P which can be obtained by intergrating $d ¯ ¯ ¯ B$ by varying the angle from $θ = Φ_{1} \to θ - Φ_{2}$ is
$¯ ¯ ¯ B = \frac{μ_{0} I}{4 π r a} \int_{Φ_{1}}^{Φ_{2}} sin θ d θ ˆ n = \frac{μ_{0} I}{4 π a} ({cos Φ}_{1} - {cos Φ}_{2}) ˆ n$
For a an infinitely long straight wire ,1=0 and 2=,the magnetic field is $¯ ¯ ¯ B = \frac{μ_{0} I}{2 π a} ˆ n ... . (3)$ Note that here $ˆ n$ represents the unit vector from the point O to P.

|

Updated on:21/07/2023

Class 12 PHYSICS SAMPLE PAPER-8

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER-8-PART-IV

Home
Ask Doubt
Profile