A particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
Let us select point projection as the origin and X- and Y-axis as shown in the figure .

There is no acceleration in the horizontal direction hence we can write the following :
x=ut⇒txu
We can use S=ut+12at2 in the Y-direction . Initial
Velocity along Y-axis is zero and acceleration a=g, as we have selected downward direction as the positive direction .
S=ut+12at2
⇒y=12gt2
Substituting t from equation (i) ,
⇒y=12g(xu)2⇒y=gx22u2
We can also write the following equation:
y=xtanθ
Substituting from equation (iii) in equation (ii) , we get the following :
xtanθ=gx22u2
⇒x=2u2gtanθ
Substituting in equation (iii) , we get the following :
y=2u2gtan2θ
Distance of the stone point of projection can be written as followings:
l=√x2+y2=2u2gtanθ√1+tan2thea
⇒l=2u2gtanθsecθ
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) NCERT (Textbook Exercises)
25 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) (NCERT (Additional Exercises))
7 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Conceptual Questions
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA pariicle is projected horizontally with a speed (u) from top of a plance inclined at anangle θ with the horizontal direction. How far from the point of projection will the particle strike the plane ?
View Solution
Knowledge Check
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
A2v2gB√2[2v2g]Cv2gD√2v2gA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
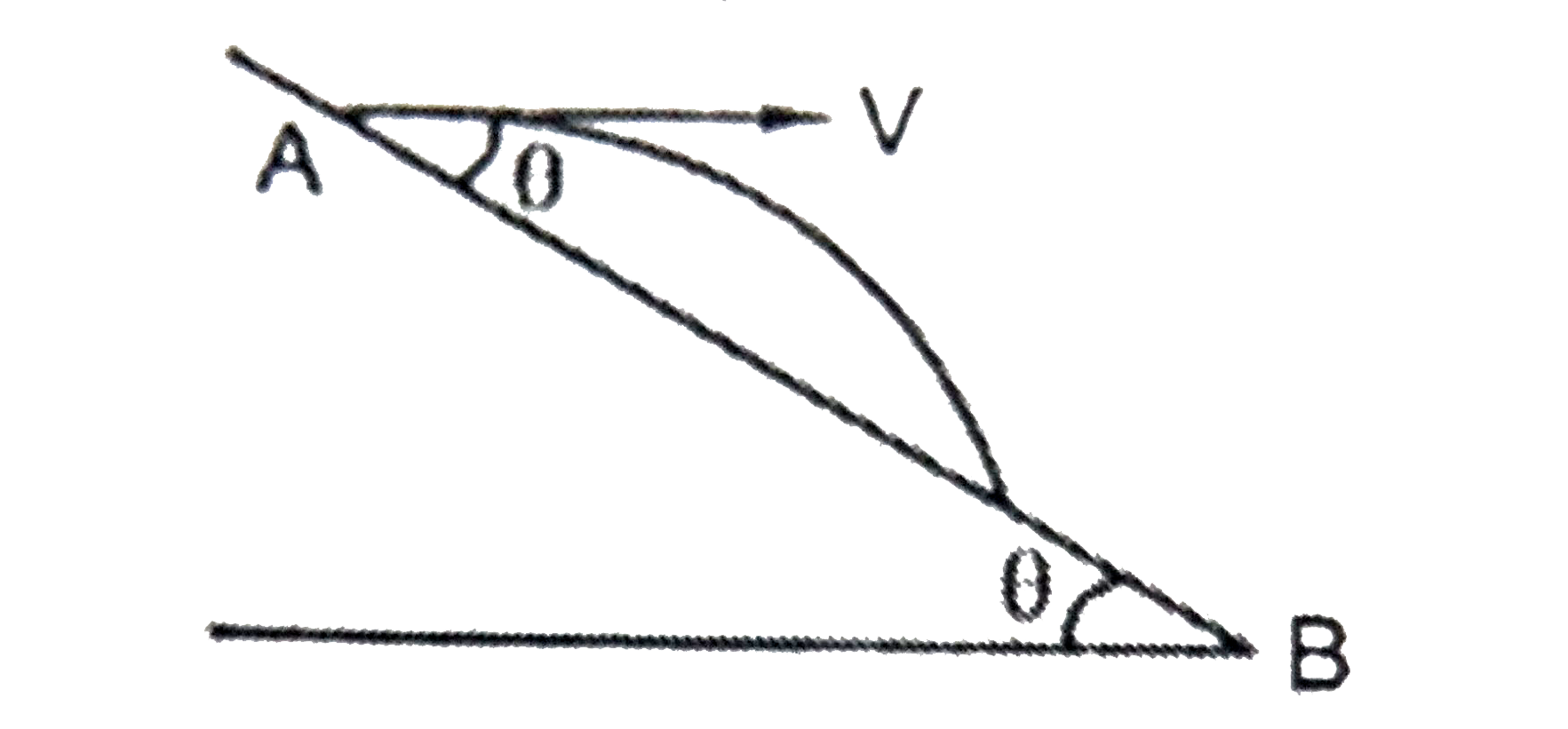
How far from the point of projection will the particle strike the plane?A75mB6516mC7516mD859mA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
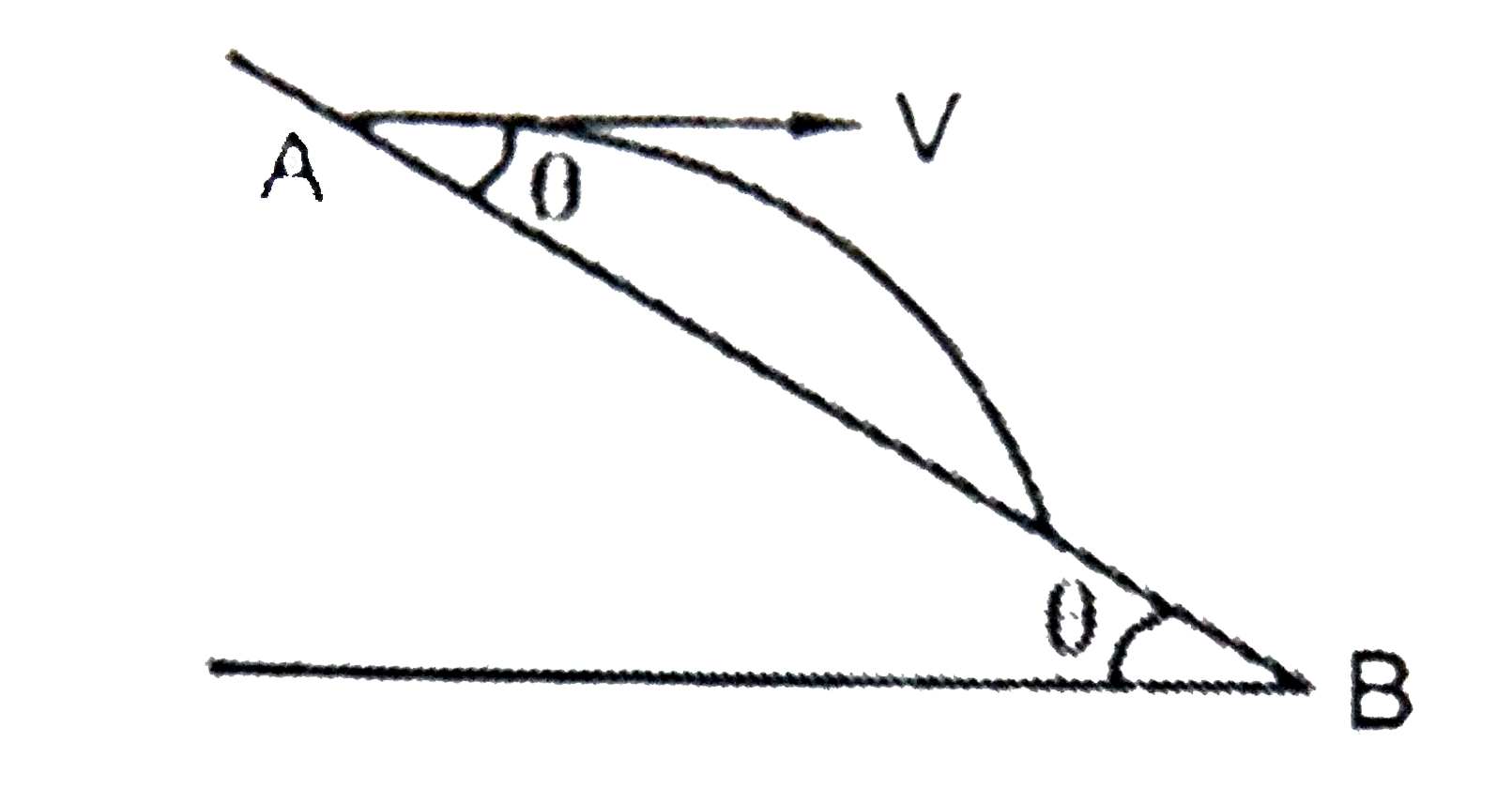
Find the time taken by the particle to hit the plane.A34sB3sC4sD43s
A particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)
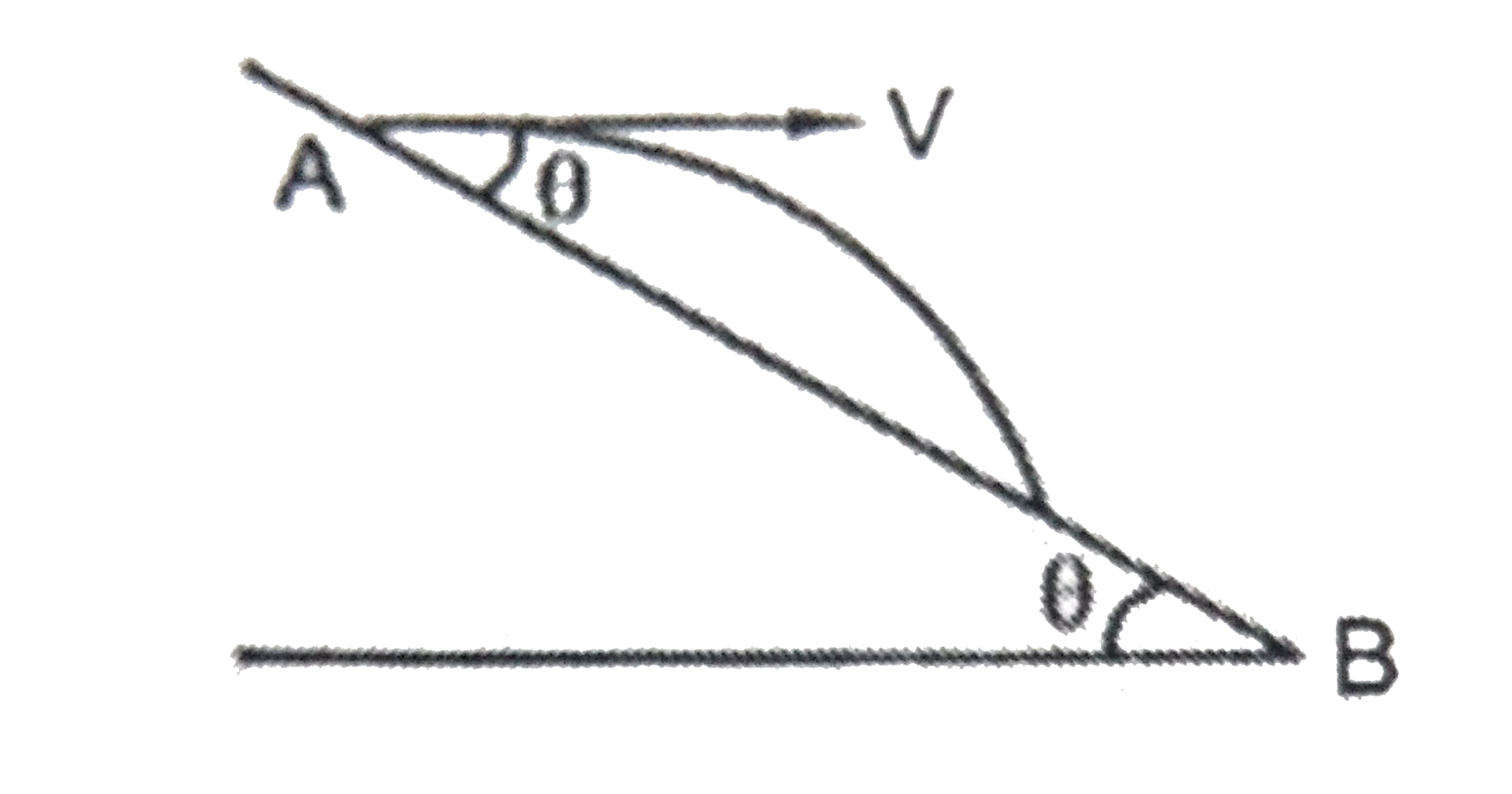
What is the velocity of the particle just before it hits the plane?
View Solution
