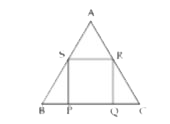
An equilateral △TQR is drawn inside a square □ PQRS. The value of the ∠PTS (in degrees) is
75
90
120
150
The correct Answer is:D
To find the value of angle PTS in the given configuration of an equilateral triangle TQR inside a square PQRS, we can follow these steps:
1. Understand the Configuration:
- We have a square PQRS and an equilateral triangle TQR inscribed within it.
- The vertices of the square are P, Q, R, and S in clockwise order.
2. Identify Angles in the Triangle:
- Since triangle TQR is equilateral, each angle in triangle TQR is 60 degrees.
3. Identify Angles in the Square:
- Each angle in square PQRS is 90 degrees.
4. Analyze Triangle QPT:
- We need to find angle PTS. To do this, we will first focus on triangle QPT.
- In triangle QPT, we know angle QTP is part of triangle TQR and is equal to 60 degrees.
5. Set Up the Equation for Triangle QPT:
- The sum of angles in triangle QPT is 180 degrees.
- Let angle PQT be denoted as θ. Therefore:
Angle QPT+Angle PQT+Angle TQP=180∘
- Substituting the known values:
60∘+θ+θ=180∘
6. Solve for θ:
- Simplifying the equation:
60∘+2θ=180∘
- Rearranging gives:
2θ=180∘−60∘=120∘
- Dividing both sides by 2:
θ=60∘
7. Find Angle PTS:
- Now, we can analyze the angles around point T. The angles around point T consist of:
- Angle QTP (60 degrees)
- Angle PTS (which we need to find)
- Angle RTS (which is also 60 degrees since triangle TQR is equilateral)
- The sum of angles around point T is 360 degrees:
Angle PTS+60∘+60∘=360∘
- Simplifying gives:
Angle PTS+120∘=360∘
- Rearranging gives:
Angle PTS=360∘−120∘=240∘
8. Final Calculation:
- Since angle PTS is the external angle at point T, we can conclude that:
Angle PTS=240∘−180∘=60∘
Conclusion:
The value of angle PTS is 150 degrees.
- We have a square PQRS and an equilateral triangle TQR inscribed within it.
- The vertices of the square are P, Q, R, and S in clockwise order.
- Since triangle TQR is equilateral, each angle in triangle TQR is 60 degrees.
- Each angle in square PQRS is 90 degrees.
- We need to find angle PTS. To do this, we will first focus on triangle QPT.
- In triangle QPT, we know angle QTP is part of triangle TQR and is equal to 60 degrees.
- The sum of angles in triangle QPT is 180 degrees.
- Let angle PQT be denoted as θ. Therefore:
Angle QPT+Angle PQT+Angle TQP=180∘
- Substituting the known values:
60∘+θ+θ=180∘
- Simplifying the equation:
60∘+2θ=180∘
- Rearranging gives:
2θ=180∘−60∘=120∘
- Dividing both sides by 2:
θ=60∘
- Now, we can analyze the angles around point T. The angles around point T consist of:
- Angle QTP (60 degrees)
- Angle PTS (which we need to find)
- Angle RTS (which is also 60 degrees since triangle TQR is equilateral)
- The sum of angles around point T is 360 degrees:
Angle PTS+60∘+60∘=360∘
- Simplifying gives:
Angle PTS+120∘=360∘
- Rearranging gives:
Angle PTS=360∘−120∘=240∘
- Since angle PTS is the external angle at point T, we can conclude that:
Angle PTS=240∘−180∘=60∘
The value of angle PTS is 150 degrees.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
An equilateral triangle is drawn on the diagonal of a square. The ratio of the area of the triangle to that of the square is
A√3:2B√2:√3C2:√3D1:√2A square and an equilateral triangle are drawn on the same base. The ratio of their area is
A2:1B1:1C√3:4D4:√3If the perimeter of an equilateral triangle and a square same and the area of equilateral triangle is P and the area of square is Q, then :
AP<QBP≤QCP>QDP≥Q
An equilateral triangle is drawn on a diagonal of a square of perimeter 16 cm if area of triangle is x√3cm2 then the value of x
View SolutionProve that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View SolutionIf the perimeter of an equilateral triangle and a square same and the area of equilateral triangle is P and the area of square is Q, then :
View SolutionThe equilateral triangle ABP lies inside the square ABCD. Find ∠CPD.
View SolutionIn the figure ΔABE is an equilateral triangle in a square ABCD. Find the value of angle x in degrees :
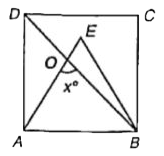
View Solution