A chord AB of a circle C1 of radius (square root 3 + 1) cm touches a circel C2 of radius (square root 3 -1) cm, then the length of AB is
8VIcm
44√3cm
4VIcm
2^/1 cm
The correct Answer is:B
To find the length of the chord AB of circle C1 that touches circle C2, we can follow these steps:
1. Identify the Radii of the Circles:
- The radius of circle C1 is r1=√3+1 cm.
- The radius of circle C2 is r2=√3−1 cm.
2. Understand the Configuration:
- Both circles are concentric, meaning they share the same center O.
- Let C be the midpoint of the chord AB.
3. Use the Pythagorean Theorem:
- The distance from the center O to the chord AB is OC which is equal to the radius of circle C2, i.e., OC=r2=√3−1.
- The distance from the center O to the endpoint of the chord A is OA, which is equal to the radius of circle C1, i.e., OA=r1=√3+1.
4. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem in triangle OAC:
OA2=OC2+AC2
- Substitute the values:
(√3+1)2=(√3−1)2+AC2
5. Calculate OA2 and OC2:
- Calculate OA2:
OA2=(√3+1)2=3+2√3+1=4+2√3
- Calculate OC2:
OC2=(√3−1)2=3−2√3+1=4−2√3
6. Substitute Back into the Equation:
- Now substitute OA2 and OC2 into the equation:
4+2√3=(4−2√3)+AC2
- Rearranging gives:
AC2=(4+2√3)−(4−2√3)=4√3
7. Find the Length of the Chord AB:
- Since AC is half of AB, we have:
AC=√4√3=2√(4)3
- Therefore, the length of the chord AB is:
AB=2×AC=2×2√(4)3=4√(4)3
Final Answer:
The length of the chord AB is 4√(4)3 cm.
- The radius of circle C1 is r1=√3+1 cm.
- The radius of circle C2 is r2=√3−1 cm.
- Both circles are concentric, meaning they share the same center O.
- Let C be the midpoint of the chord AB.
- The distance from the center O to the chord AB is OC which is equal to the radius of circle C2, i.e., OC=r2=√3−1.
- The distance from the center O to the endpoint of the chord A is OA, which is equal to the radius of circle C1, i.e., OA=r1=√3+1.
- According to the Pythagorean theorem in triangle OAC:
OA2=OC2+AC2
- Substitute the values:
(√3+1)2=(√3−1)2+AC2
- Calculate OA2:
OA2=(√3+1)2=3+2√3+1=4+2√3
- Calculate OC2:
OC2=(√3−1)2=3−2√3+1=4−2√3
- Now substitute OA2 and OC2 into the equation:
4+2√3=(4−2√3)+AC2
- Rearranging gives:
AC2=(4+2√3)−(4−2√3)=4√3
- Since AC is half of AB, we have:
AC=√4√3=2√(4)3
- Therefore, the length of the chord AB is:
AB=2×AC=2×2√(4)3=4√(4)3
The length of the chord AB is 4√(4)3 cm.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
The circle C1 of radius (√3+1) has chord AB which touch another circle C2 which is concentric to C1. If radius of C2 is (√3−1) then length of AB (in cm) will be.
A24√3cmB8√3cmC44√3cmD4√4cmThe chord of circle whose radius is 5 cm touches another circle radius is 3 cm. If two circles are concentric, then what is length of chord?
Aa)10 cmBb)12.5 cmCc)8 cmDd)7 cmIf a chord of a circle of radius 5 cm is a tangent to another circle of radius 3 cm, both the circles being concentric, then the length of the chord is
A10 cmB12.5 cmC8 cmD7 cm
There are two concentric circles with centre O and a chord AB of outer circle cut the inner circle at C and D. If distance of chord to centre is 3 cm, outer radius is 13 cm and inner radius is 7 cm, then length of AC is-
View SolutionO is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
View SolutionIf a square ABCD is inscribed in a circle of radius 'r' and AB = 4 cm, then the value of r is :
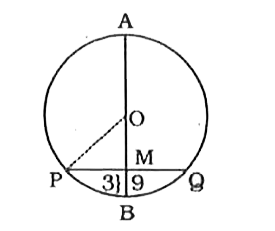
View SolutionIn a given circle, the chord PQ is of length 18 cm. AB is the perpendicular bisector of PQ at M. If MB=3cm, then the length of AB is
View SolutionEF is a chord of a circle whose length is 10 cm. If radius of the circle is 13 cm, then the length of perpendicular from the centre to the chord is
View Solution
