AB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
34∘
124∘
56∘
68∘
To solve the problem step by step, we will follow the geometric properties of circles and triangles.
1. Identify the Given Information:
- AB is a diameter of the circle with center O.
- C is a point on the circumference of the circle.
- The tangent at point C meets the extended line of AB at point Q.
- We are given that ∠CAB=34∘.
2. Understand the Geometry:
- Since AB is a diameter, by the Inscribed Angle Theorem, any angle subtended by the diameter at the circumference (in this case, angle ACB) is a right angle. Therefore, ∠ACB=90∘.
3. Apply the Triangle Angle Sum Property:
- In triangle ACB, the sum of the angles is 180∘. Thus, we can write:
∠CAB+∠ACB+∠CBA=180∘
- Substituting the known angles:
34∘+90∘+∠CBA=180∘
4. Simplify the Equation:
- Combine the known angles:
124∘+∠CBA=180∘
5. Solve for ∠CBA:
- Isolate ∠CBA:
∠CBA=180∘−124∘
∠CBA=56∘
6. Conclusion:
- The measure of ∠CBA is 56∘.
Final Answer:
The measure of ∠CBA is 56∘.
- AB is a diameter of the circle with center O.
- C is a point on the circumference of the circle.
- The tangent at point C meets the extended line of AB at point Q.
- We are given that ∠CAB=34∘.
- Since AB is a diameter, by the Inscribed Angle Theorem, any angle subtended by the diameter at the circumference (in this case, angle ACB) is a right angle. Therefore, ∠ACB=90∘.
- In triangle ACB, the sum of the angles is 180∘. Thus, we can write:
∠CAB+∠ACB+∠CBA=180∘
- Substituting the known angles:
34∘+90∘+∠CBA=180∘
- Combine the known angles:
124∘+∠CBA=180∘
- Isolate ∠CBA:
∠CBA=180∘−124∘
∠CBA=56∘
- The measure of ∠CBA is 56∘.
The measure of ∠CBA is 56∘.
Topper's Solved these Questions
Similar Questions
AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?
View SolutionIn the adjoining figure AB is a diameter of the circle with centre 0 .If ∠BOD=15∘and∠EOA=85∘ the measure of ∠ECA is
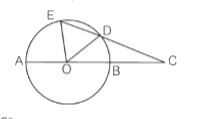
View Solution
Knowledge Check
AB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
A56∘B34∘C68∘D124∘AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?A5∘B7∘C17∘D6∘A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘
In the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB ?
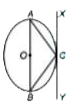
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB?

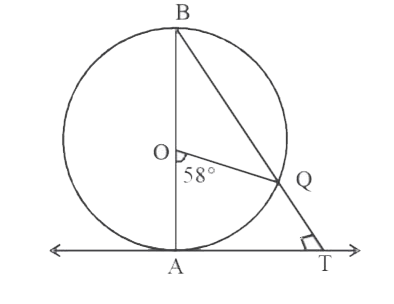
View SolutionAB is a diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘ find ∠ATQ.
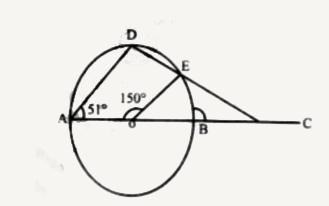
View SolutionIn the following figures, AB be diameter of a circle whose centre is O. If ∠AOE=150∘,∠DAO=51∘, then the measure of ∠CBE is-
View SolutionAB and AC are tangents to the circle with centre O. Then x equals.
View Solution
