In Fig.A and B are identical radiators of waves that are in phase and of the same wavelength .The radiators are rotated by distance in , d = 3.00 .The greatest distance from A, along the x - axis, for which fully destructive interference occurs is :
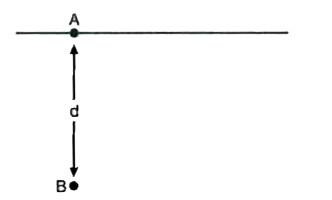 .
.
The correct Answer is:A
Squaring, we get
Now
Solving, .

Topper's Solved these Questions
- WAVE OPTICS Book:MODERN PUBLICATIONChapter:WAVE OPTICS Exercise:MCQ LEVEL -1 (ASSERTIONS)
Explore 3 Videos
- WAVE OPTICS Book:MODERN PUBLICATIONChapter:WAVE OPTICS Exercise:MCQ LEVEL -1 (PARAGRAPH QUESTIONS )
Explore 34 Videos
- WAVE MOTIONBook:MODERN PUBLICATIONChapter:WAVE MOTIONExercise:RECENT COMPETITIVE QUESTIONS
Explore 18 Videos
- WORK , POWER , ENERGY AND COLLISIONSBook:MODERN PUBLICATIONChapter:WORK , POWER , ENERGY AND COLLISIONSExercise:Revision Test
Explore 40 Videos
Similar Questions
Two coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
View SolutionFor Bragg's diffraction by a crystal to occur, then the X-ray of wavelength λ and interatomic distance d must be
View Solution
Knowledge Check
Two coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
 A3λB8λC5λ/4D8.75λ
A3λB8λC5λ/4D8.75λFor Bragg's differaction by a crystal to occur, then the X-ray of wavelength λ and ineratomic distance d must be
Aλ is greater than 2dBλ equals 2dCλ is smaller than or equal to 2dDλis smaller than 2dFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along
 A(a) Path 1B(b) Path 2C(c) Any pathD(d) None of these
A(a) Path 1B(b) Path 2C(c) Any pathD(d) None of these
In Figure, two isotropic point sources S1 and S2 emit light in phase at wavelength λ and at the same amplitude. The sources are separated by distance 2d=6.00λ. They lie on an axis that is parallel to an x axis, which runs along a viewing screen at distance D=20.0λ. The origin lies on the perpendicular bisector between the sources. The figure shows two rays reaching point P on the screen, at position xP. (a) At what value of xP do the rays have the minimum possible phase difference? (b) What multiple of λ gives that minimum phase difference? (c) At what value of xP do the rays have the maximum possible phase difference? What multiple of λ gives (d) that maximum phase difference and (c) the phase difference when xP=6.00λ? (f) When xP=6.00λ, is the resulting intensity at point P maximum, minimum, intermediate but closer to maximum, or intermediate but closer to minimum?
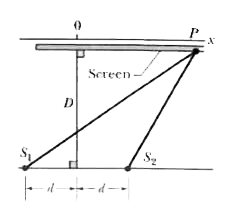
View SolutionThe equation of line belonging to the family of lines (5x+3y−2)+λ(3x−y−4)=0,λ∈R ,and at greatest distance from (0,0) is
View SolutionFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along

View SolutionFour monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
View SolutionA and B are two points on water surface where waves are generated. What is the phase diff. if
(i) A and B are on same wavefront separated by distance λ.
(ii) A and B are on successive crests separated by distance 2λ.
(iii) A and B are on successive troughs separated by distance 3λ.
View Solution
