Find the distance between adjacent interference bands if the distance from the source to biprism is 1 m and from biprism to screen is 4 m.The angle of refraction of biprism is 2×10−3 rad. How many interference bands can be observed on the screen ?
(Given μ=1.5 & λ=6000Å)

A

5

B

4

C

3

D

2

Text Solution
Verified by Experts

The correct Answer is:A

d=2(μ−1).A.L=2(1.5−1)×2×10−3×1=2×10−3m
ocr_image
D=4+1=5m
β=λ.Dd=15×10−4 m
If N = number of fringes
Then N=Lβ, where L is width of interference pattern
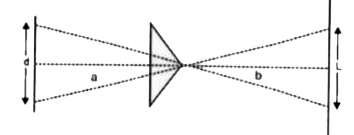
From fig.
Ld=ba
∴L=ba×d=41×2×10−3=8×10−3
N=8×10−315×10−4=5.3≈5.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSWAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In a biprism experiment the distance of source from biprism is 1 m and the distance of screen from biprism is 4 meters. The angle of refraction of biprism is 2×10−3 radians. μ of biprism is 1.5 and the wavelength of light used is 6000 Å. How many fringes will be seen on the screen ?

    A4
    B5
    C3
    D6

  • In Fresnel's biprism (μ=1.5) experiment the distance between source and biprism is 0.3m and that between biprism and screen is 0.7m and angle of prism is 1∘. The fringe width with light of wavelength 6000Å will be

    A(a) 3cm
    B(b) 0.011cm
    C(c) 2cm
    D(d) 4cm

  • The distance between the slit and the biprism and between the biprims and the screen 50 cm each. The angle of the biprism is 179∘ and its refractive index is 1.5. If the distance between successive bright fringes is 0.0135cm, then the wavelenghts of lights is

    A5893×10−10cm
    B5898×10−8cm
    C5898×10−8m
    D2946×10−8cm