The distance between the slit and biprism and screen and biprism are 50 cm each.The obtuse angle of biprism is $179^{\circ}$ and its refractive index is 1.5. If the distance between successive fringes is 0.135 mm, the wavelength of light used is :

A

$5893 Å$

B

$11786 Å$

C

$2946 Å$

D

$6574 Å$

Text Solution

Verified by Experts

The correct Answer is:B

$α + 179 + α = 180^{\circ}$
$α = \frac{0.5 π}{180^{\circ}} r a d$
$d = 2 a (μ - 1) α$

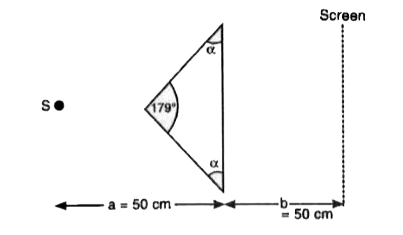
Solving , $d = \frac{0.25 π}{180} m$
$\Rightarrow β = \frac{D . λ}{d} = 5834 Å$
Then $λ = 11786 Å$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The distance between the slit and the biprism and between the biprims and the screen 50 cm each. The angle of the biprism is $179^{\circ}$ and its refractive index is $1.5$ . If the distance between successive bright fringes is $0.0135 c m$ , then the wavelenghts of lights is
A $5893 \times 10^{- 10} c m$
B $5898 \times 10^{- 8} c m$
C $5898 \times 10^{- 8} m$
D $2946 \times 10^{- 8} c m$
Question 2 - Select One
In a biprism experimentn the distance between the two virtual images of the slits is 7 mm and the distance between slit adnd eyepiece is 1 m. If the distance between two consecurtive bright band is $0.1$ then the wavelength of lights is
A $7000 Å$
B $6500 Å$
C $6000 Å$
D $5000 Å$
Question 3 - Select One
In a double slit interference experiment, the distance between the slits is 0.05 cm and screen is 2m away from the slits. The wavelength of light is $8.0 \times 10^{- 5}$ cm. The distance between successive fringes is
A0.24 cm
B3.2 cm
C1.28 cm
D0.32 cm

MODERN PUBLICATION-WAVE OPTICS -MCQ LEVEL- II

Home
Ask Doubt
Profile