A circle is circumscribed around a square as shown in the figure. The area of one of the four shaded portions is equal to 47 . The radius of the circle is (FIGURE) √2 (b) 1√2 (c) 2 (d) 3
To solve the problem step by step, let's break it down as follows:
Step 1: Understand the relationship between the circle and the square
A circle is circumscribed around a square, which means that the circle touches all four corners of the square. If we denote the radius of the circle as r and the side length of the square as a, we can relate these two using the formula:
a=r√2
This is because the diagonal of the square is equal to the diameter of the circle.
Hint: Remember that the diagonal of a square can be calculated using the Pythagorean theorem.
Step 2: Calculate the area of the square and the area of the circle
The area of the square Asquare is given by:
Asquare=a2=(r√2)2=2r2
The area of the circle Acircle is given by:
Acircle=πr2
Hint: Use the formulas for the area of a square and a circle to find their respective areas.
Step 3: Find the area of the shaded regions
The area of one of the four shaded regions can be calculated by subtracting the area of the square from the area of the circle and then dividing by 4 (since there are four shaded regions):
Ashaded=14(Acircle−Asquare)=14(πr2−2r2)
This simplifies to:
Ashaded=14((π−2)r2)
Hint: Remember to divide the total shaded area by 4 to find the area of one shaded region.
Step 4: Set up the equation with the given area of the shaded region
We know from the problem that the area of one shaded region is equal to 47:
14(π−2)r2=47
Multiplying both sides by 4 gives:
(π−2)r2=167
Hint: Isolate r2 by dividing both sides by (π−2).
Step 5: Solve for r2
Rearranging gives:
r2=167(π−2)
Hint: Substitute the value of π (approximately 3.14) to evaluate r2.
Step 6: Find r
To find r, take the square root of both sides:
r=√167(π−2)
Step 7: Evaluate to find the numerical value of r
Using π≈3.14:
π−2≈1.14
Thus:
r2≈167×1.14≈167.98≈2
So,
r≈√2
Final Answer: The radius of the circle is √2.
A circle is circumscribed around a square, which means that the circle touches all four corners of the square. If we denote the radius of the circle as r and the side length of the square as a, we can relate these two using the formula:
a=r√2
This is because the diagonal of the square is equal to the diameter of the circle.
The area of the square Asquare is given by:
Asquare=a2=(r√2)2=2r2
The area of the circle Acircle is given by:
Acircle=πr2
The area of one of the four shaded regions can be calculated by subtracting the area of the square from the area of the circle and then dividing by 4 (since there are four shaded regions):
Ashaded=14(Acircle−Asquare)=14(πr2−2r2)
This simplifies to:
Ashaded=14((π−2)r2)
We know from the problem that the area of one shaded region is equal to 47:
14(π−2)r2=47
Multiplying both sides by 4 gives:
(π−2)r2=167
Rearranging gives:
r2=167(π−2)
To find r, take the square root of both sides:
r=√167(π−2)
Using π≈3.14:
π−2≈1.14
Thus:
r2≈167×1.14≈167.98≈2
So,
r≈√2
Topper's Solved these Questions
Similar Questions
In the adjoining figure, if the radius of each of the four outer circles is r , what is the radius of the inner circle? (FIGURE) (a) 2√2+1r (b) 1√2r (c) (√2−1)r (d) √2 r
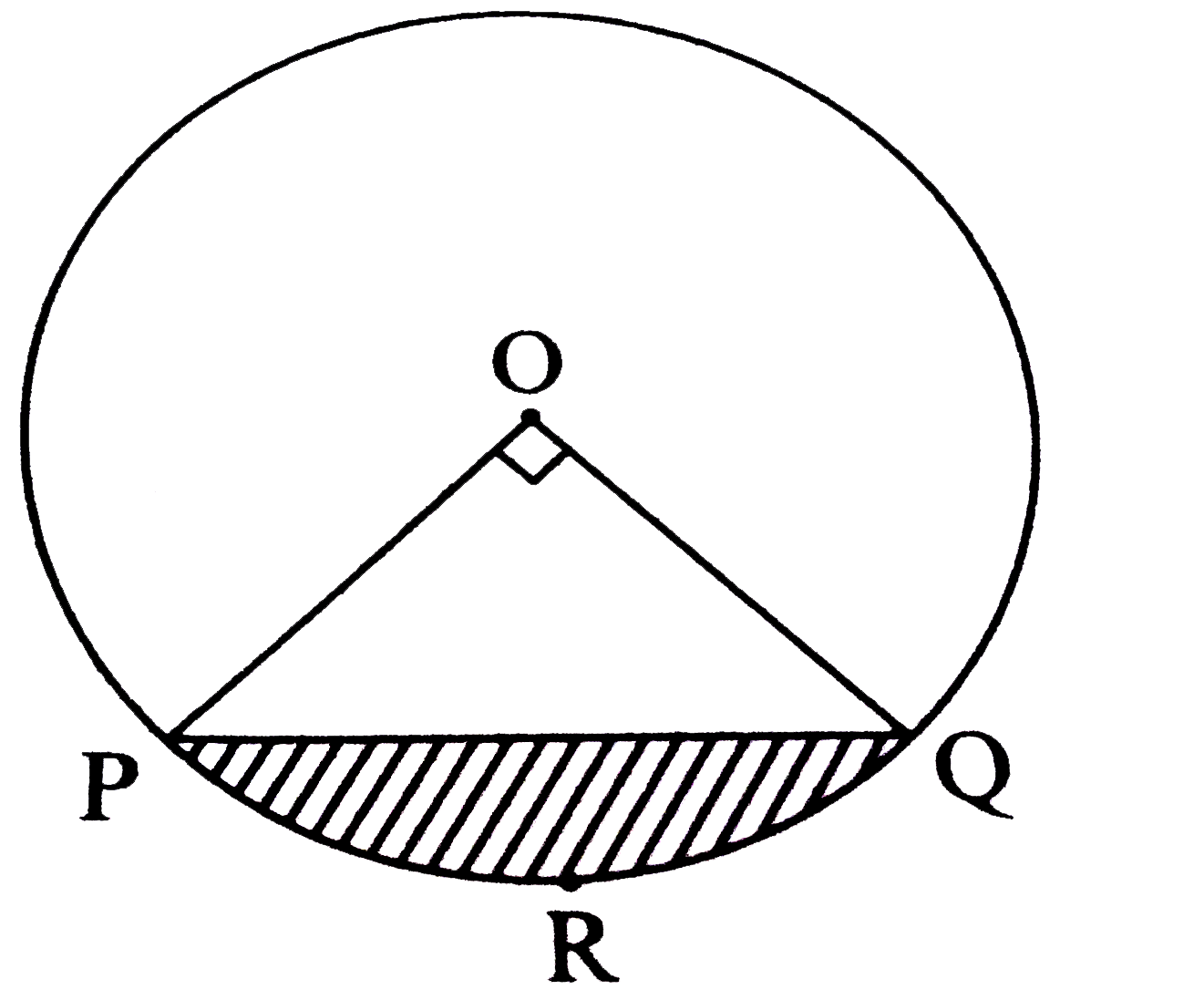
View SolutionIn the figure, O is the centre of the circle. ∠POQ=90∘ .
The area of the shaded region is 126cm2. Find the radius of the circle.
View Solution
Knowledge Check
X and Y are the centres of 2 circles on a square as shown in the figure. What is the area of the shaded portion ? (Take π=3.14)
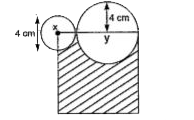 A25.12cm2B28.26cm2C71.74cm2D88cm2
A25.12cm2B28.26cm2C71.74cm2D88cm2In the following figure, if PQ=R (P is the centre of the bigger circle) and the shaded area is equal to A, then the radius of the inner circle is equal to -
 A(πR−A)B√(πR−Aπ)C√R−AπD√R2−Aπ
A(πR−A)B√(πR−Aπ)C√R−AπD√R2−AπThree circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ?
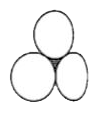 A(2√3−π2)cm2B(3√2−π3)cm2C2√3πcm2Dnone of the above
A(2√3−π2)cm2B(3√2−π3)cm2C2√3πcm2Dnone of the above
The area of a square is equal to the area of a circle. The ratio between the side of the square and the radius of the circle is (a) √π:1 (b) 1:√π (c) 1:π (d) π:1
View SolutionUsing figure 8.2, the ratio of the area of the shaded portion to that of the whole figure is ______.
View SolutionA circle is inscribed in a square of side 54 cms and another circle circumscribes the same square. Then the ratio of circumferences of the bigger circle to the smaller circle is 1 :√2 (b) √2 :1 (c) √3 :1 (d) None of these
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4. The radius of the circle is 3√5 (b) 5√3 (c) 2√5 (d) 5√2
View SolutionABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is 2−√2 (b) √2−1 1/2 (d) 1√2
View Solution
