In the adjoining figure, if the radius of each of the four outer circles is r , what is the radius of the inner circle? (FIGURE) (a) 2√2+1r (b) 1√2r (c) (√2−1)r (d) √2 r
Step by step video & image solution for In the adjoining figure, if the radius of each of the four outer circles is r , what is the radius of the inner circle? (FIGURE) (a) 2/(sqrt(2)+1)r (b) 1/(sqrt(2))r (c) (sqrt(2)-1)r (d) sqrt(2)\ r by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the adjoining figure, if the radius of each of the four outer circles is r , what is the radius of the inner circle? (FIGURE) (a) 2√2+1r (b) 1√2r (c) (√2−1)r (d) √2 r
View SolutionA circle is circumscribed around a square as shown in the figure. The area of one of the four shaded portions is equal to 47 . The radius of the circle is (FIGURE) √2 (b) 1√2 (c) 2 (d) 3
View Solution
Knowledge Check
In the figure, when the outer circles all have radii 'r', then the radius of the inner circle will be
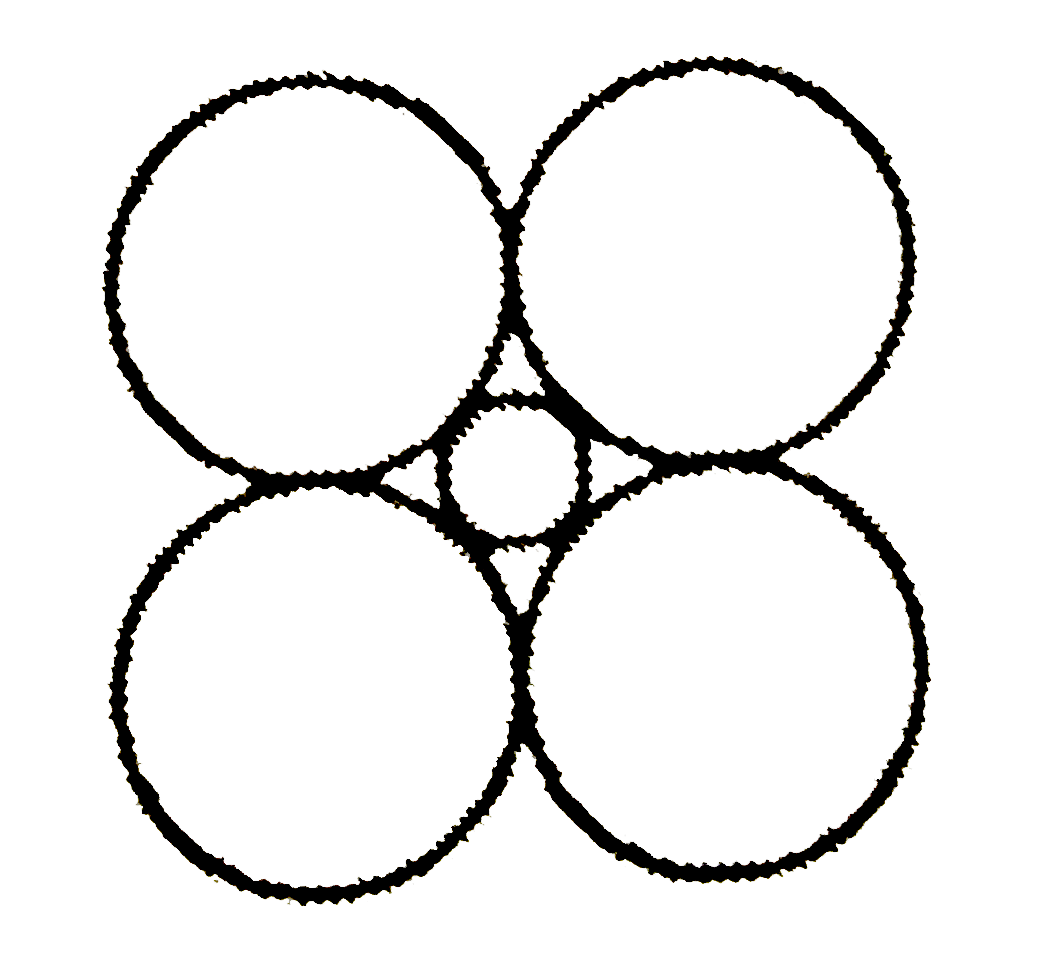 A√2rB(√2−1)rC1√2rD2(√2−1)r
A√2rB(√2−1)rC1√2rD2(√2−1)rThree circles of radius 1 cm are circumscribed by a circle of radius r, as shown in the figure. Find the value of r?
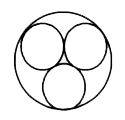
(a)√3+1
(b)2+√3√3
(c)√3+2√2
(d)2+√3A√3+1B2+√3√3C√3+2√2D2+√3If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
AR1+R2=RBR21+R22=R2CR1+R2<RDR21+R22<R2
The equation of four circles are (x±a)2+(y±a2=a2 . The radius of a circle touching all the four circles is (√2+2)a (b) 2√2a (√2+1)a (d) (2+√2)a
View SolutionIn the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
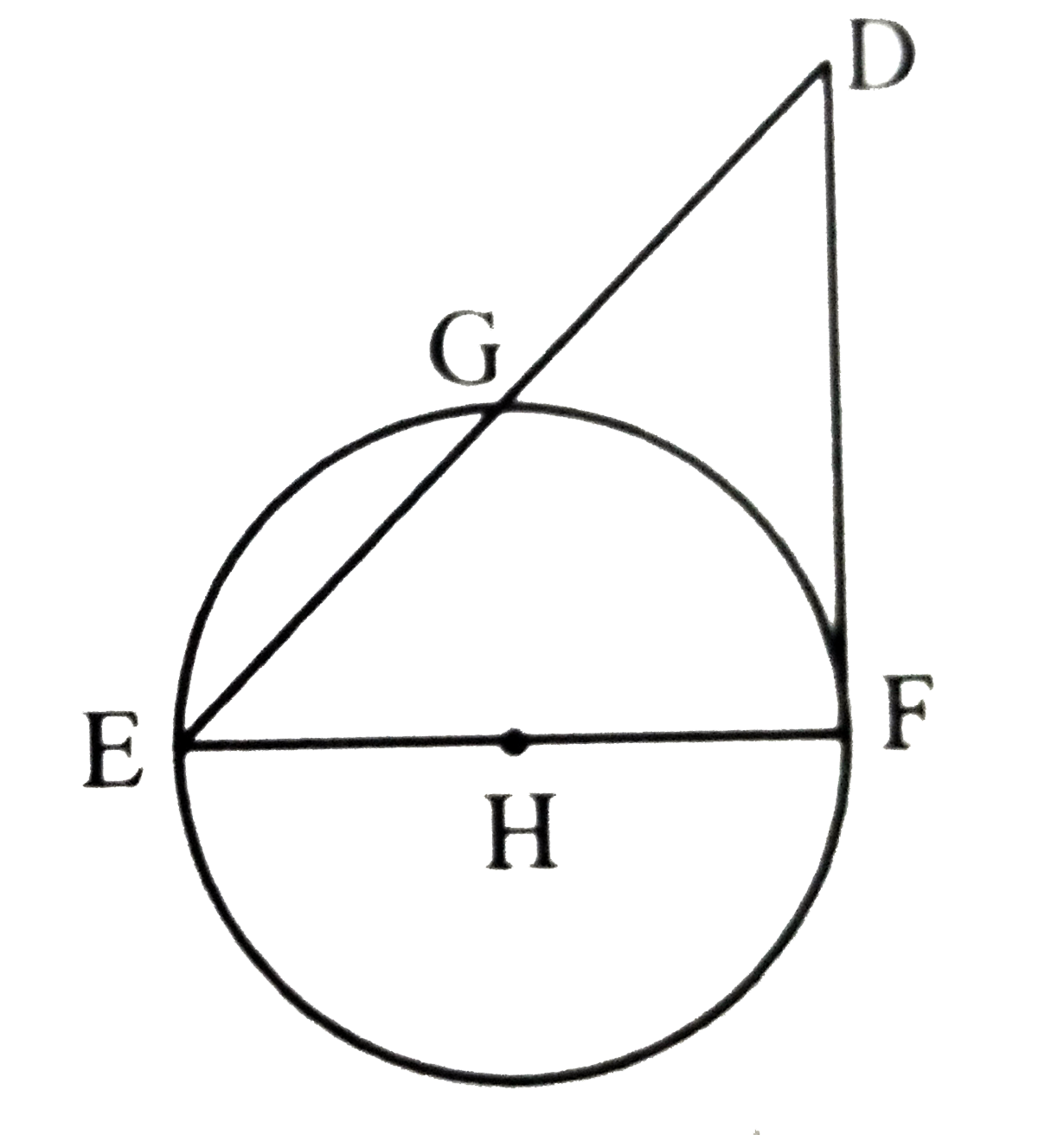
View Solution1 If r and R be the radii of inner and outer circles respectively, then area of ring is
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionTwo equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circles is √r (b) √2 r AB (c) √3 r (d) √32 rLet the two circles have their centres at AandC.
View Solution