Let Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
−1<α<0
0<α<1
0≤α≤1
−1≤α<0
The correct Answer is:A
Step by step video, text & image solution for Let P_n(ix) =1+2x+3x^2+............+(n+1)x^n be a polynomial such that n is even.The number of real roots of P_n(x)=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise30videos
MISCELLANEOUS EQUATIONS AND INEQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test21videos
MEASURES OF CENTRAL TENDENCY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test31videos
PLANE AND STRAIGHT LINE IN SPACE
Similar Questions
Knowledge Check
- Question 1 - Select One
The maximum number of real roots of the equation x2n−1=0, is
A2B3CnD2n - Question 2 - Select One
If p(x) is a n degree polynomial the number of roots are
A1B2C3Dn - Question 3 - Select One
Let P(x) be a polynomial such that p(x)-p'(x)= xn, where n is a positive integer. Then P(0) equals-
An!B(n-1)!C1n!D1(n−1)!
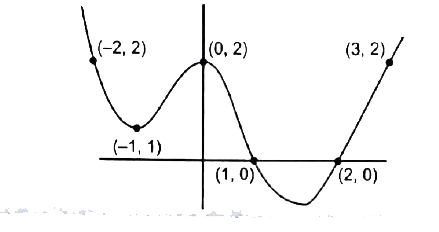
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
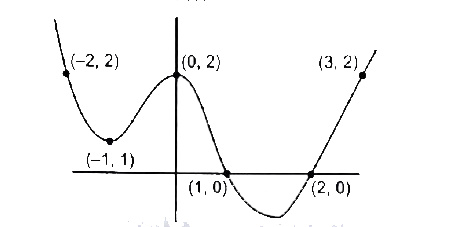
The product of all imaginary roots of p(x)=0 is:View SolutionLet n be a positive integer with f(n)=1!+2!+3!+.........+n!andp(x),Q(x) be polynomial in x such that f(n+2)=P(n)f(n+1)+Q(n)f(n) for all n≥, Then
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
The number of real roots of the equation, (x−1)2+(x−2)2+(x−3)2=0 isView SolutionA polynomial p(x)=aoxn+a1xn−1+....+an−1x+an,a0≠0 is said to be a reciprocal equation if ai=an−i for 0≤i≤[n2] where [x] denote the greatest integer≤x. If p(x) is a reciprocal polynomial of odd degree, then one of the roots of p(x) = 0 is
View SolutionLet Pn(u) be a polynomial is u of degree n. Then, for every positive integern, sin2nx is expressible is
View Solution