Let Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
Step by step video & image solution for Let P_n(ix) =1+2x+3x^2+............+(n+1)x^n be a polynomial such that n is even.The number of real roots of P_n(x)=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If p(x) is a n degree polynomial the number of roots are
A1B2C3DnLet P(x) be a polynomial such that p(x)-p'(x)= xn, where n is a positive integer. Then P(0) equals-
An!B(n-1)!C1n!D1(n−1)!
In the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
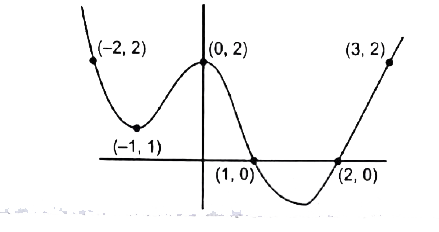
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.

The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
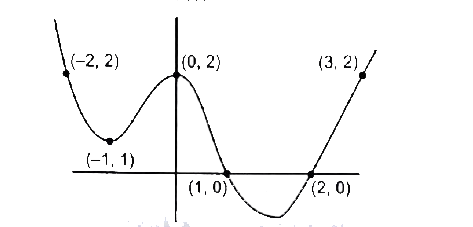
The product of all imaginary roots of p(x)=0 is:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.

The product of all imaginary roots of p(x)=0 is:
View SolutionLet n be a positive integer with f(n)=1!+2!+3!+.........+n!andp(x),Q(x) be polynomial in x such that f(n+2)=P(n)f(n+1)+Q(n)f(n) for all n≥, Then
View SolutionLet n be a positive integer with f(n)=1!+2!+3!+.........+n!andp(x),Q(x) be polynomial in x such that f(n+2)=P(n)f(n+1)+Q(n)f(n) for all n≥, Then
View Solution
