In a rectangle ABCD, AB= 15 cm ∠BAC=60∘ then BC is equal to
15√3
15√32
15√3
152√3
The correct Answer is:A
To solve the problem, we need to find the length of side BC in rectangle ABCD, given that AB = 15 cm and angle BAC = 60°.
1. Identify the triangle: In rectangle ABCD, we can focus on triangle ABC. Here, AB is one side, and we need to find the length of side BC.
2. Use the tangent function: We know that in triangle ABC, angle BAC is given as 60°. We can use the tangent function, which relates the opposite side to the adjacent side in a right triangle. The formula for tangent is:
tan(θ)=oppositeadjacent
In this case, angle BAC = 60°, the opposite side is BC, and the adjacent side is AB.
3. Substitute the known values: We can substitute the values we have into the tangent formula:
tan(60°)=BCAB
Given that AB = 15 cm, we have:
tan(60°)=BC15
4. Calculate tan(60°): The value of tan(60°) is √3. Therefore, we can rewrite the equation:
√3=BC15
5. Solve for BC: To find BC, we can multiply both sides by 15:
BC=15⋅√3
6. Final answer: Thus, the length of BC is:
BC=15√3 cm
Summary:
The length of side BC in rectangle ABCD is 15√3 cm.
tan(θ)=oppositeadjacent
In this case, angle BAC = 60°, the opposite side is BC, and the adjacent side is AB.
tan(60°)=BCAB
Given that AB = 15 cm, we have:
tan(60°)=BC15
√3=BC15
BC=15⋅√3
BC=15√3 cm
The length of side BC in rectangle ABCD is 15√3 cm.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - PRACTICE SET EXERCISE - PRACTICE SET-550videos
PRACTICE SET
- BOOK - ARIHANT SSCCHAPTER - PRACTICE SET EXERCISE - PRACTICE SET-350videos
PRACTICE SET
- BOOK - ARIHANT SSCCHAPTER - PIPES AND CISTERNS EXERCISE - EXERCISE HIGHER SKILL LEVEL QUESTION17videos
PIPES AND CISTERNS
- BOOK - ARIHANT SSCCHAPTER - PROBABILITYEXERCISE - EXERCISE (LEVEL-2)19videos
PROBABILITY
Similar Questions
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
View SolutionIn a △ABC, AD is perpendicular to BC from A, if ∠BAC=90∘, then AB2:AC2 is equal to :
त्रिभुज ABC में, AD, A से BC पर डाला गया लम्ब है | यदि ∠BAC=90∘ है, तो AB2:AC2 का मान क्या होगा ?View Solution
Knowledge Check
- Question 1 - Select One
In a rectangle ABCD , AB = 15 cm and ∠BAC=60∘, then the length of side BC is
A15√2 cmB15 cmC15√5 cmD15√3 cm - Question 2 - Select One
In a right angled ΔABC,∠C=90∘andCD is the perpendicular on hypotenuse AB if BC = 15 cm and AC=20cm then CD is equal to :
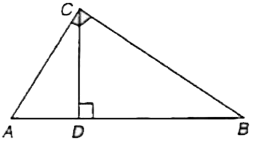 A18 cmB12 cmC17.5 cmDcan't be determined
A18 cmB12 cmC17.5 cmDcan't be determined - Question 3 - Select One
In ΔABC, D is a point on side BC such that ∠ADC=∠BAC, If CA = 12 cm, CB = 8 cm then CD is equal to :
A18 cmB12 cmC16 cmD15 cm
ABCD is a rombus in which angle C = 60∘. Then, BC : AD is equal to
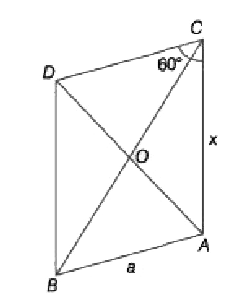 View Solution
View SolutionIn a rectangle ABCD, AB=20cm , ∠BAC=60o . Calculate side BC .
View Solution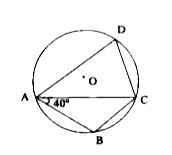
In the figure given above, O is the centre of a circle circumscribing a quadrilateral ABCD. If AB=BC and ∠BAC=40∘, then what is ∠ADC equal to ?View SolutionIn ΔABC, right-angled at B, AB = 3 cm and ∠BAC =60∘ . Determine the lengths of the sides BC and AC.
View SolutionA paper is in the form of a rectangle ABCD where AB = 21 cm and BC = 14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining paper
View Solution

