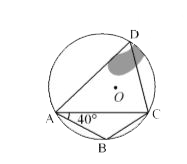
In the figure given above, O is the centre of a circle circumscribing a quadrilateral ABCD. If AB=BC and ∠BAC=40∘, then what is ∠ADC equal to ?
50∘
60∘
70∘
80∘
Step by step video & image solution for In the figure given above, O is the centre of a circle circumscribing a quadrilateral ABCD. If AB = BC and /_BAC = 40^@, then what is /_ADC equal to ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
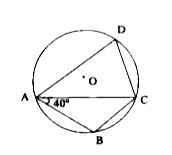
ABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD=140∘and ∠BAC=40∘. then the value of ∠BCD is equal to
A70∘B90∘C60∘D80∘In a rectangle ABCD, AB= 15 cm ∠BAC=60∘ then BC is equal to
A15√3B15√32C15√3D152√3ABCD is a cycle quadrilateral such that is the diameter of the circle circumscribing it and ∠ADC=150∘. Then, ∠BAC is equal to :
A60∘B50∘C40∘D38∘
In Figure, O is the centre of the circle. Find ∠BAC
View Solution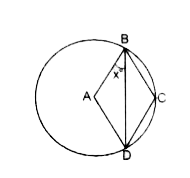
In the figure given above, A is the centre of the circle and AB = BC = CD. What is the value of x ?
View SolutionThe area of a cyclic quadrilateral ABCD is 3√34 . The radius of the circle circumscribing cyclic quadrilateral is 1.If AB=1 and BD=√3, then BC⋅CD is equal to
View Solution
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯BC and ¯¯¯¯¯¯CD are equal chords. If ∠OBC=70∘ , then find ∠BAD.
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
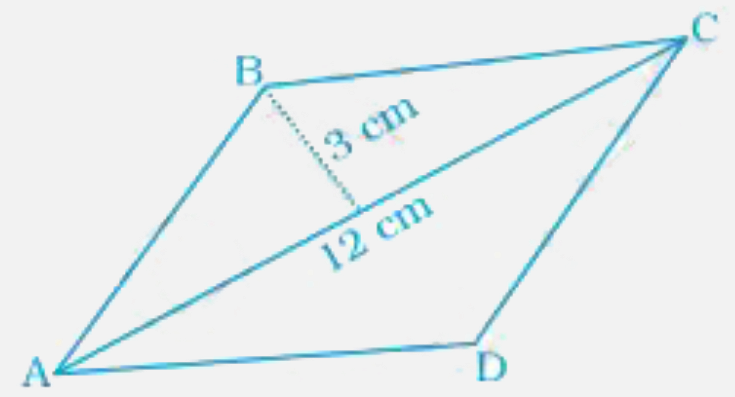
View Solution