A rectangular block has length 10 cm, breadth 8 cm and height 2 cm. From this block , a cubical hole of side 2 cm is drilled out . Find the volume and the surface area of the remaining solid :
152cm3,512cm2
125cm3,215cm2
152cm3,240cm2
125cm3,512cm2
The correct Answer is:C
To solve the problem, we need to find the volume and surface area of the remaining solid after drilling a cubical hole from a rectangular block. Let's break down the solution step by step.
Step 1: Calculate the Volume of the Rectangular Block
The formula for the volume V of a rectangular block is given by:
V=Length×Breadth×Height
Given:
- Length L=10cm
- Breadth B=8cm
- Height H=2cm
Calculating the volume:
V=10×8×2=160cm3
Step 2: Calculate the Volume of the Cubical Hole
The volume Vc of a cube is given by:
Vc=Side3
Given:
- Side of the cube s=2cm
Calculating the volume of the cube:
Vc=23=8cm3
Step 3: Calculate the Remaining Volume
To find the remaining volume Vr after drilling the hole, we subtract the volume of the cube from the volume of the rectangular block:
Vr=V−Vc=160−8=152cm3
Step 4: Calculate the Surface Area of the Rectangular Block
The formula for the surface area SA of a rectangular block is given by:
SA=2(LB+BH+HL)
Calculating each term:
- LB=10×8=80
- BH=8×2=16
- HL=2×10=20
Now substituting these values into the surface area formula:
SA=2(80+16+20)=2(116)=232cm2
Step 5: Adjust the Surface Area for the Drilled Hole
When a cube is drilled out, we lose the area of the faces that were part of the block but gain the area of the new faces created inside the hole. The cube has 6 faces, but since we are drilling it out, we will add back the area of 2 faces (the top and bottom of the hole).
The area of one face of the cube is:
Area of one face=s2=22=4cm2
Thus, the area of two faces is:
Area of two faces=2×4=8cm2
Now, the new total surface area SAr of the remaining solid is:
SAr=SA+Area of two faces=232+8=240cm2
Final Results
- Remaining Volume: 152cm3
- Remaining Surface Area: 240cm2
Summary
The volume of the remaining solid is 152cm3 and the surface area is 240cm2.
The formula for the volume V of a rectangular block is given by:
V=Length×Breadth×Height
Given:
- Length L=10cm
- Breadth B=8cm
- Height H=2cm
V=10×8×2=160cm3
The volume Vc of a cube is given by:
Vc=Side3
Given:
- Side of the cube s=2cm
Vc=23=8cm3
To find the remaining volume Vr after drilling the hole, we subtract the volume of the cube from the volume of the rectangular block:
Vr=V−Vc=160−8=152cm3
The formula for the surface area SA of a rectangular block is given by:
SA=2(LB+BH+HL)
Calculating each term:
- LB=10×8=80
- BH=8×2=16
- HL=2×10=20
SA=2(80+16+20)=2(116)=232cm2
When a cube is drilled out, we lose the area of the faces that were part of the block but gain the area of the new faces created inside the hole. The cube has 6 faces, but since we are drilling it out, we will add back the area of 2 faces (the top and bottom of the hole).
Area of one face=s2=22=4cm2
Thus, the area of two faces is:
Area of two faces=2×4=8cm2
SAr=SA+Area of two faces=232+8=240cm2
- Remaining Volume: 152cm3
- Remaining Surface Area: 240cm2
The volume of the remaining solid is 152cm3 and the surface area is 240cm2.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.6
40 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.7
12 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.4
25 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
From a solid cylinder of height 36 cm and radius 14 cm a conical cavity of radus 7 cm and height 24 cm is drilled out . Find the volume and the total surface area of the remaining solid.
View SolutionThe volume of a rectangular glass slab of length= 3 cm, breadth 2 cm and height 2 cm is____cm3
View Solution
Knowledge Check
A rectangular block has length 10 cm, breadth 8 cm and height 2 cm. From this block , a cubical hole of side 2 cm is drilled out . Find the volume and the surface area of the remaining solid :
A152cm3,512cm2B125cm3,215cm2C152cm3,240cm2D125cm3,512cm2In the given figure from a cuboidal solid metallic block of dimensions 15cm×10cm×5cm a cylindrical hole of diamter 7 cm is drilled out . Find the suface area of the remaining block .
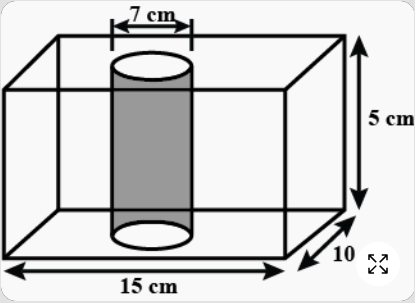 A450cm2B553cm2C550cm2D583cm2
A450cm2B553cm2C550cm2D583cm2
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 is hollwed out. Find the volume of the remaining solid.
View SolutionThe length , breadth and height of a cuboidal shaped box of medicine is 20 cm , 12 cm and 10 cm respectively . Find the total surface area of the box .
View SolutionA rectangular block of length 20 cm, breadth 15 cm and height 10 cm is cut up into exact number of equal cubes. The least possible number of cubes will be
View SolutionThe height of a solid cylindr is 15 cm and diameter is 7 cm .Two equal conical holes of radius 3 cm and height 4 cm are cut off . Find the volume and surface area of the solid.
View SolutionFrom a solid cylinder of height 4cm and radius 3cm a conical cavity of height 4cm of base radius 3cm is hollowed out. What is the total surface area of the remaining solid?
View SolutionFrom a solid cylinder whose height is 8 cm and radius 6cm , a conical cavity of height 8 cm and of base radius 6 cm is hollowed out . Find the volume of the remaining solid.Also find the total surface area of the reamining solid.[ Take π=3.14 ]
View Solution
