A circle is drawn on AB as diameter. The centre of the circle is O and the length AB = 13 cm. P is a point on the circumference of the cirlces such that the chord AP = 12 cm. Calculate the value of the angles PAB and POB in radians :
0.395,0.789
0.786,0.735
0.389.0.689
0.786,0.753
The correct Answer is:A
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the given information
- The diameter AB=13cm
- The length of the chord AP=12cm
- The center of the circle O
Step 2: Calculate the radius of the circle
Since AB is the diameter, we can find the radius r of the circle:
r=AB2=132=6.5cm
Step 3: Use the Pythagorean theorem in triangle APB
In triangle APB, we can apply the Pythagorean theorem since ∠APB is a right angle (angle in a semicircle):
AB2=AP2+PB2
Substituting the known lengths:
132=122+PB2
Calculating the squares:
169=144+PB2
Rearranging gives:
PB2=169−144=25
Taking the square root:
PB=√25=5cm
Step 4: Calculate angle PAB
Now we can find angle PAB using the tangent function:
tan(PAB)=PBAP=512
To find PAB:
PAB=tan−1(512)
Calculating this gives:
PAB≈0.395radians
Step 5: Calculate angle POB
Since O is the center of the circle, angle POB is twice angle PAB:
POB=2×PAB=2×0.395≈0.790radians
Summary of Results
- PAB≈0.395radians
- POB≈0.790radians
- The diameter AB=13cm
- The length of the chord AP=12cm
- The center of the circle O
Since AB is the diameter, we can find the radius r of the circle:
r=AB2=132=6.5cm
In triangle APB, we can apply the Pythagorean theorem since ∠APB is a right angle (angle in a semicircle):
AB2=AP2+PB2
Substituting the known lengths:
132=122+PB2
Calculating the squares:
169=144+PB2
Rearranging gives:
PB2=169−144=25
Taking the square root:
PB=√25=5cm
Now we can find angle PAB using the tangent function:
tan(PAB)=PBAP=512
To find PAB:
PAB=tan−1(512)
Calculating this gives:
PAB≈0.395radians
Since O is the center of the circle, angle POB is twice angle PAB:
POB=2×PAB=2×0.395≈0.790radians
- PAB≈0.395radians
- POB≈0.790radians
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - TRIGONOMETRYEXERCISE - INTRODUCTORY EXERCISE - 11.218videos
TRIGONOMETRY
- BOOK - ARIHANT SSCCHAPTER - TRIGONOMETRYEXERCISE - INTRODUCTORY EXERCISE - 11.315videos
TRIGONOMETRY
- BOOK - ARIHANT SSCCHAPTER - TRIGONOMETRYEXERCISE - Higher Skill Level Questions34videos
TRIGONOMETRY
- BOOK - ARIHANT SSCCHAPTER - TIME, SPEED AND DISTANCEEXERCISE - SPEED TEST (TSD)10videos
TIME, SPEED AND DISTANCE
- BOOK - ARIHANT SSCCHAPTER - TRUE DISCOUNT AND BANKER'S DISCOUNTEXERCISE - FAST TRACK PRACTICE23videos
TRUE DISCOUNT AND BANKER'S DISCOUNT
Similar Questions
Knowledge Check
- Question 1 - Select One
AB is a diameter of radius 4.5 cm circle. P is any point on the circumference of circle such that PN⊥AB. If length of chord PB is 6 cm . Then BN = ?
A5 cmB4 cmC6 cmD4.5 cm - Question 2 - Select One
AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
A17 cmB15 cmC4 cmD8 cm - Question 3 - Select One
In the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘
AD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is
View SolutionThe chord of length 12 cm is at a distance of √13cm from the centre of the circle. Area of this circle is
View SolutionCalculate the distance (in cm) of the chord from the centre of the circle, if the chord of length 48 cm is drawn in the circle of radius 25 cm.
View SolutionO' is the centre of the circle, AB is a chord of the circle, OM⊥AB. If AB=20cm,OM=2√11 cm, then radius of the circle is
View SolutionIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
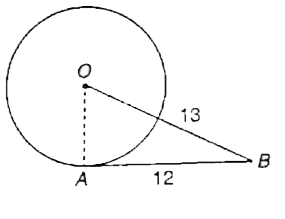 View Solution
View Solution

