In the ΔABC,BD bisects ∠B, and is prpendicular to AC. If the lengths of the sides of the triangle are expressed in the terms of x and y as shown, find the value of x and y :
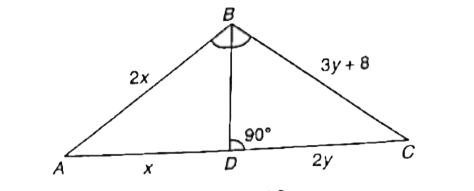
6,12
10,12
16,8
8,15
The correct Answer is:C
Step by step video, text & image solution for In the DeltaABC, BD bisects angleB, and is prpendicular to AC. If the lengths of the sides of the triangle are expressed in the terms of x and y as shown, find the value of x and y : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.328videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC, if ∠A=60∘,∠B=50∘,and∠C=70∘, then find the longest side of the triangle ABC.
ABCBABCACDNone of these
The sides of a triangle are x,yandz. if x+y=7,y+z=9andz+x=8.then find the area of the triangle.
View SolutionFind the vertices and the area of the triangle whose sides are x=y,y=2xandy=3x+4.
View SolutionIf the angles of a triangle are x, y and 40∘ and the difference between the two angles x and y is 30∘. Then, find the value of x and y.
View SolutionOne side of an equilateral triangle is 3x+4y=7 and its vertex is (1,2). Then the length of the side of the triangle is
View SolutionExpress y in terms of x in the expression 3x–7y=10
View SolutionThe equations of the perpendicular bisectors of the sides AB&AC of a triangle ABC are x−y+5=0&x+2y=0. find the equation of the bc
View SolutionIn a triangle, the sum of lengths of two sides is x and the product of the lengths of the same two sides is y. If x2−c2=y, where c is the length of the third side of the triangle, then the circumradius of the triangle is c√k. The value of k is _________.
View Solution

