Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
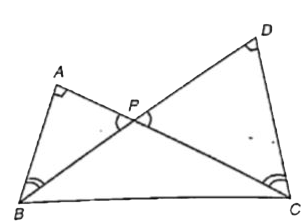
APPC=BPDP
AP×DP=PC×BP
AP×PC=BP×DP
AP×BP=PC×PD
The correct Answer is:C
Step by step video, text & image solution for Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.328videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Two triangles BACandBDC , right angled at AandD respectively, are drawn on the same base BC and on the same side of BC . If AC and DB intersect at P, prove that AP⋅PC=DP⋅PB.
View SolutionTwo triangles ABC and DBC are on the same base BC and on the same side of BC in which ∠A=∠D=90∘. If CAandBD meet each other at E, show that AE.EC=BE.ED.
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.
 View Solution
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
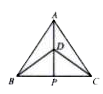
ΔABD≅ΔACDView SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
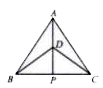
ΔABP≅ΔACPView SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
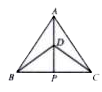
AP bisects ∠A as well as ∠D.View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
 View Solution
View Solution

