The bisector of the exterior ∠A of ΔABC intersects the side BC produced to D. Here CF is parallel to AD.
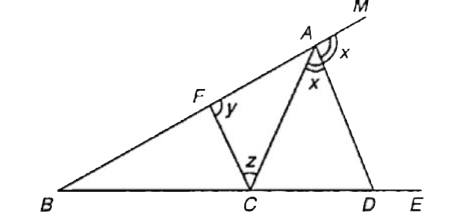
ABAC=BDCD
ABAC=CDBD
ABAC=BCCD
none of these
The correct Answer is:A
Step by step video, text & image solution for The bisector of the exterior angleA of DeltaABC intersects the side BC produced to D. Here CF is parallel to AD. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.328videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
In a ΔABC,∠C in an obtuse angle . The bisectors of the exterior angles at A and B meet BC and AC produced at D and E respectively . If AB=AD=BE. Find ∠ACB .
View SolutionIn a triangle ABC, the sides AB, AC are produced and the bisectors of exterior angles of ∠ABCand∠ACB intersect at D. If ∠BAC=50∘, then ∠BDC is equal to
View Solution
Knowledge Check
- Question 1 - Select One
In a ΔABC,∠C in an obtuse angle . The bisectors of the exterior angles at A and B meet BC and AC produced at D and E respectively . If AB=AD=BE. Find ∠ACB .
A105∘B108∘C110∘D135∘ - Question 2 - Select One
The bisector of ∠A of ΔABC cuts BC at D and the circumcircle of the triangle at E. then
AAB:AC=BD:DCBAD:AC=AE:ABCAB:AD=AC:AEDAB:AB=AE:AC - Question 3 - Select One
In the figure AD is the external bisector of ∠EAC, intersects BC produced to D. IF AB=12cm,AC=8cmandBC=4cm, find CD :
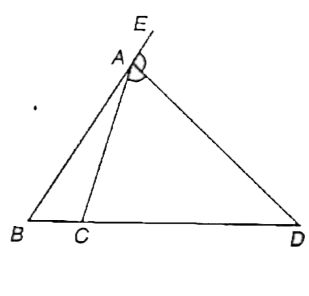 A10 cmB6 cmC8 cmD9 cm
A10 cmB6 cmC8 cmD9 cm
In a ΔABC,∠C in an obtuse angle . The bisectors of the exterior angles at A and B meet BC and AC produced at D and A respectively . If AB=AD=BE. Find ∠ACB .
View SolutionThe bisector of interior ∠Aof△ABC meets BC in D, and the bisector of exterior angle ∠Ameets BC produced in E. prove that BDBE=CDCE
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
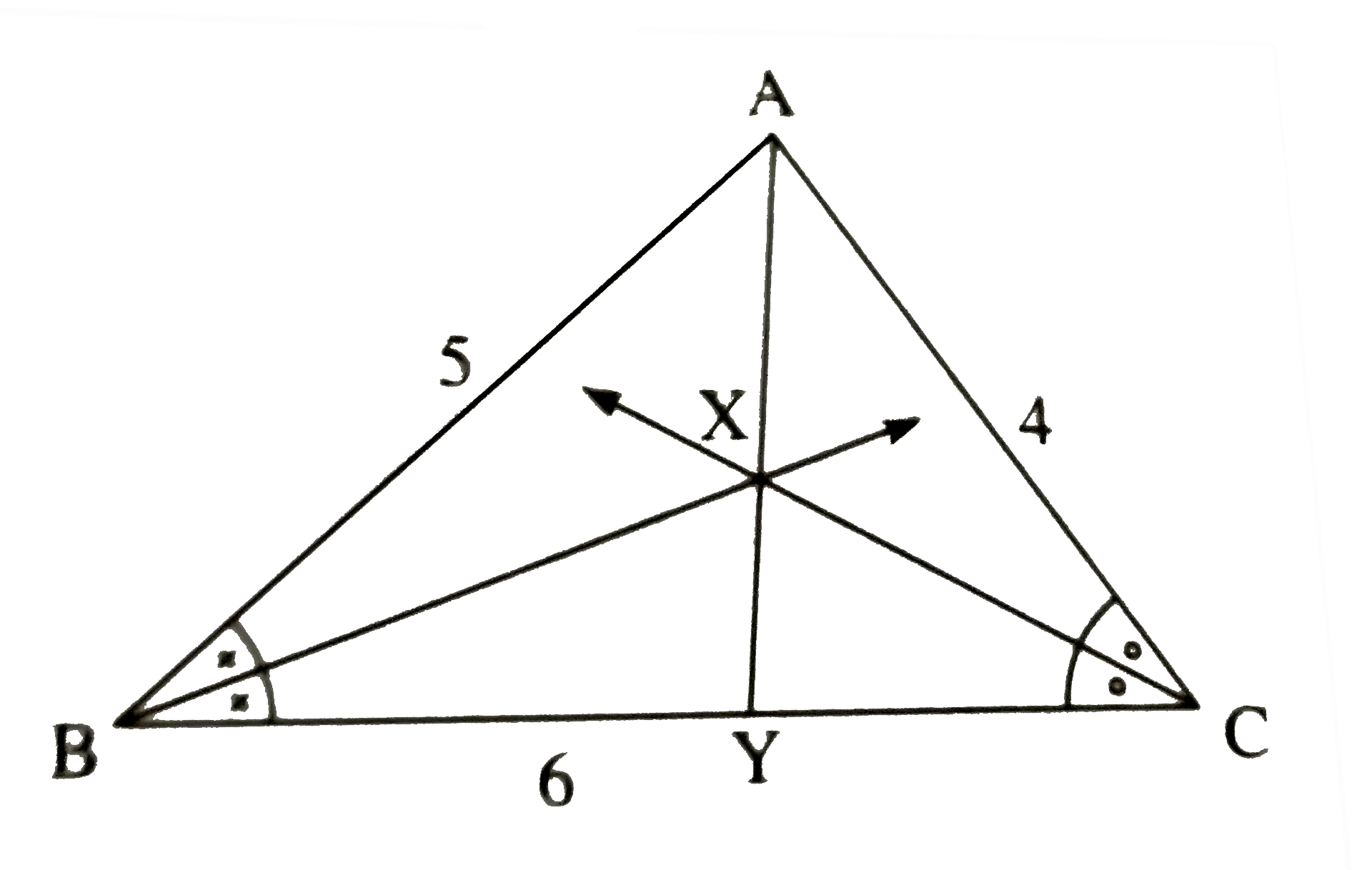
View SolutionIn the figure bisectors of ∠B and ∠C of ΔABC intersect each other in point X. Line AX intersects side BC in pont Y. AB=5,AC=4,BC=6 then find AXXY
 View Solution
View SolutionIn the figure AD is the external bisector of ∠EAC, inttersects BC produced to D. If AB=12cmandBC=4cm, find CD.
View Solution

