Question

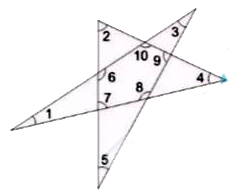
What is the sum of all the angles of a 9 pointed star $(\text{i.e.,}\angle 1+\angle 2+\angle 3+\dots ..\angle 8+\angle 9)$

Options

A. `909^(@)`
B. `900^(@)`
C. `720^(@)`
D. `540^(@)`

Answer

B

Explanation

To find the sum of all the angles of a 9-pointed star, we can follow these steps:

Step 1: Identify the formula for the sum of angles in a star
The formula for the sum of the angles of an n-pointed star is given by:
\( \text{Sum of angles} = (n - 4) \times 180 \)
where \( n \) is the number of points in the star.

Step 2: Substitute the value of \( n \)
In this case, we have a 9-pointed star, so we substitute \( n = 9 \) into the formula:
\( \text{Sum of angles} = (9 - 4) \times 180 \)

Step 3: Perform the subtraction
Calculate \( 9 - 4 \):
\( 9 - 4 = 5 \)

Step 4: Multiply by 180
Now, multiply the result by 180:
\( \text{Sum of angles} = 5 \times 180 \)

Step 5: Calculate the final result
Now, calculate \( 5 \times 180 \):
\( 5 \times 180 = 900 \)

Final Answer
Thus, the sum of all the angles of a 9-pointed star is:
\( \text{Sum of angles} = 900 \)

---