ABCD is a square, in which a circle is inscribed touching all the sides of square. In the four corners of square 4 smaller circles of equal radii are drawn, containing maximum possible area.
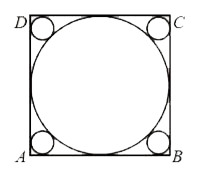
What is the ratio of the area of larger circle to that of sum of the areas of four smaller circles?
(a) 1:(68−48√2)
(b)1:17√2
(c)3:(34−12√2)
(d)None of these
1:(68−48√2)
1:17√2
3:(34−12√2)
none of these
The correct Answer is:A
Step by step video & image solution for ABCD is a square, in which a circle is inscribed touching all the sides of square. In the four corners of square 4 smaller circles of equal radii are drawn, containing maximum possible area. What is the ratio of the area of larger circle to that of sum of the areas of four smaller circles? (a) 1 : (68 - 48 sqrt2) (b)1 : 17 sqrt2 (c)3 : (34 - 12 sqrt2) (d)None of these by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A circle is inscribed in a square and the area of square is 784 cm2. Find the area of the circle.
A154cm2B308cm2C616cm2D1232cm2A square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
A1:1B1:4Cπ:2Dπ:4A square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
A1:1B1:4Cπ:2Dπ:4
If the perimeter of a circle and a square are equal, then what is the ratio of the area of the circle to that of the square ?
View Solutionone circle is inscribbed in a square with area "9pi" then area of square?
View SolutionA square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
View SolutionIf the area of a circle is 220cm2, then area of a square inscribed in this circle is
View SolutionA circle is inscribed in a square of side 14 m. The ratio of the area of the circle and that of the square is ______.
View Solution
