In the following diagram A and B are the centres of the two different circles.
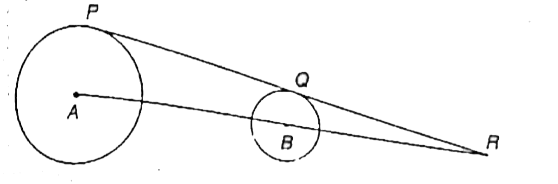
PQR is a common tangent. Poinis A, B, and R lie on the straight line.
Distance between A and B is 25 cm and the distance between P and Q is 24 cm. Diameter of the larger circle is 24 cm.
What is the ratio of area of ΔAPR and ΔBQR ?
A. 169:36
A. 144:25
B. 625:144
D. can't be determined
The correct Answer is:B
Step by step video & image solution for In the following diagram A and B are the centres of the two different circles. PQR is a common tangent. Poinis A, B, and R lie on the straight line. Distance between A and B is 25 cm and the distance between P and Q is 24 cm. Diameter of the larger circle is 24 cm. What is the ratio of area of DeltaAPR and DeltaBQR ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the following diagram A and B are the centres of the two different circles.
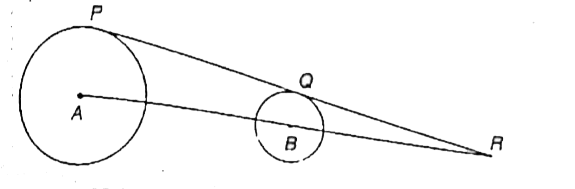
PQR is a common tangent. Poinis A, B, and R lie on the straight line.
Distance between A and B is 25 cm and the distance between P and Q is 24 cm. Diameter of the larger circle is 24 cm.
What is the ratio of AB:BR ?
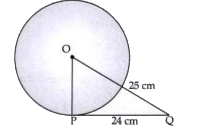
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
View Solution
Knowledge Check
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm, the radius of the circle is
A7 cmB12 cmC15 cmD24.5 cmThe length of the direct common tangent of two circles of radii 2 cm and 8 cm is 8 cm. Then the distance between the centres of the circles is
A8 cmB10 cmC6 cmD12 cmTwo circles touch internally and their centres are O and Oc as shown. The sum of their areas is 180π sq. cm. and the distance between their centres is 6 cm.
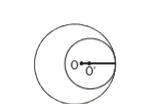
What is the diameter of the larger circle ?Aa) 16 cmBb) 12 cmCc) 18 cmDd) 24 cm
On a map,a distance of 800 km between two point A and B is represented by 12 cm .what is the actual distance between A and B if they are 24 cm a part on the map
View SolutionWhat is the distance between two parallel tangents of a circle of radius 4 cm?
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
View SolutionThe length of a chord of a circle at a distance of 5 cm from the centre is 24 cm. The diameter of the circle is
View SolutionFrom a point A, the length of the tangent to ta circle is 24 cm . And the distance of a from the centre is 25 cm . The radius of the circle is
View Solution
