A truck is staitonary and has a bob suspended by a lilght string in a frame attached to the truck The truck , suddenly moves to the right with an acceleration of a. The pendulum will tilt
to the left and angle of inclination of the penudlum with the verticle is sin−1(ga)
to the left and angle of inclination of the pendulm with the verticle is tan−1(αg)
to the left and angle of inclination of the pendulum with the veritcal is sin−1(ag)
to the left and angle of inclination of the pendulum with the veritcal is tan−19ga)
The correct Answer is:C
To solve the problem of the pendulum tilting when the truck accelerates, we will analyze the forces acting on the bob of the pendulum and apply Newton's laws of motion. Here’s a step-by-step solution:
Step 1: Understand the Setup
The truck is stationary initially, and a bob is suspended from a light string. When the truck accelerates to the right with acceleration a, the bob will experience a force due to inertia that will cause it to tilt.
Hint: Visualize the scenario and identify the forces acting on the bob.
Step 2: Identify Forces Acting on the Bob
1. Weight of the bob (mg): Acts downward.
2. Tension in the string (T): Acts along the string towards the point of suspension.
3. Inertial force: When the truck accelerates, the bob appears to experience a pseudo force to the left (equal to ma) due to its inertia.
Hint: Draw a free body diagram showing these forces.
Step 3: Set Up the Equations of Motion
We can resolve the forces acting on the bob into two components:
- In the horizontal direction (x-axis): The component of tension Tsinθ must balance the inertial force ma.
- In the vertical direction (y-axis): The component of tension Tcosθ must balance the weight of the bob mg.
Hint: Write down the equations based on the components of forces.
Step 4: Write the Equations
1. For the horizontal direction:
Tsinθ=ma(1)
2. For the vertical direction:
Tcosθ=mg(2)
Hint: Remember that θ is the angle the pendulum makes with the vertical.
Step 5: Divide the Equations
To eliminate T, divide equation (1) by equation (2):
TsinθTcosθ=mamg
This simplifies to:
tanθ=ag
Hint: This step helps to relate the angle θ to the acceleration a and gravitational acceleration g.
Step 6: Solve for θ
Now, we can find the angle θ:
θ=tan−1(ag)
Hint: This angle indicates how much the pendulum tilts from the vertical.
Step 7: Determine the Direction of Tilt
Since the truck is accelerating to the right, the bob will tilt to the left from the vertical position.
Hint: Visualize the direction of tilt based on the forces acting on the bob.
Final Answer
The pendulum will tilt to the left with an angle given by:
θ=tan−1(ag)
The truck is stationary initially, and a bob is suspended from a light string. When the truck accelerates to the right with acceleration a, the bob will experience a force due to inertia that will cause it to tilt.
1. Weight of the bob (mg): Acts downward.
2. Tension in the string (T): Acts along the string towards the point of suspension.
3. Inertial force: When the truck accelerates, the bob appears to experience a pseudo force to the left (equal to ma) due to its inertia.
We can resolve the forces acting on the bob into two components:
- In the horizontal direction (x-axis): The component of tension Tsinθ must balance the inertial force ma.
- In the vertical direction (y-axis): The component of tension Tcosθ must balance the weight of the bob mg.
1. For the horizontal direction:
Tsinθ=ma(1)
2. For the vertical direction:
Tcosθ=mg(2)
To eliminate T, divide equation (1) by equation (2):
TsinθTcosθ=mamg
This simplifies to:
tanθ=ag
Now, we can find the angle θ:
θ=tan−1(ag)
Since the truck is accelerating to the right, the bob will tilt to the left from the vertical position.
The pendulum will tilt to the left with an angle given by:
θ=tan−1(ag)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition file (Multiple choice question) JEE (Main) & Other State Boards for Engineering Entrance25videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (JEE (Advanced) For IIT Entrance)7videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions)20videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
Similar Questions
An automobile and a truck start from rest at the same instant, with the automobile initially at some distance behind the truck. The truck has a constant acceleration of 2.2m/s2 and the automobile has an acceleration of 3.5m/s2. The automobile overtakes the truck when it (truck) has moved 60 m.
(a) How much time does it take the automobile to overtake the truck ?
(b) How far was the automobile behind the truck initially ?
(c) What is the speed of each during overtaking ?View SolutionA toy truck T at rest, has a hemispherical trough of radius R in it [O is the centre of the hemisphere]. A small block A is kept at the bottom of the trough. The truck is accelerated horizontally with an acceleration a. (i) Find the minimum value of a for which the block is able to move out of the trolley. (ii) If magnitude of a is twice the minimum value found in (i), find the maximum height (measured from its original level at the bottom of the trough) to which the block will rise.
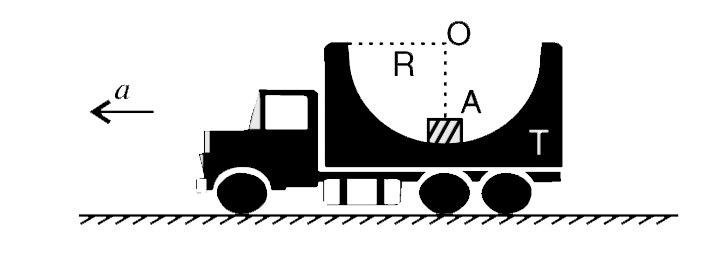 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck
 AThe particle will execute SHMBThe time period of oscillations will be 2π√mk(Cthe amplitude of oscillations will be (m2a20)DThe energy of oscillatioins will be m2a20k
AThe particle will execute SHMBThe time period of oscillations will be 2π√mk(Cthe amplitude of oscillations will be (m2a20)DThe energy of oscillatioins will be m2a20k - Question 2 - Select One or More
A block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in the figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truj starts moving towards right with a constant acceleration a0. If the block is observed from the truck
 Athe block will execute SHMBthe time period of oscillations of block will be 2π√mkCthe amplitude of oscillation of block will be ma0kDthe energy of oscillations of block will be m2a20k
Athe block will execute SHMBthe time period of oscillations of block will be 2π√mkCthe amplitude of oscillation of block will be ma0kDthe energy of oscillations of block will be m2a20k - Question 3 - Select One
In fig a sphere of mass 2 kg is suspended from the ceiling of a car which is initially at rest. Tension in the string in this situation is T1 The car now moves to the right with a uniform acceleration and the tension in the string is now T2 then: (Take g=10m/s2)
 AT1=T2=20NBT1=20N,T2>20NCT1=20N,T2<20NDT1<20N,T2=20N
AT1=T2=20NBT1=20N,T2>20NCT1=20N,T2<20NDT1<20N,T2=20N
In the figure a smooth pulley of negligible weight is suspended by a spring balance. Weights of 1kg and 5 kg are attached to the opposite ends of a string passing over the pulley and move with acceleration because of gravity. During the motion, the spring balance reads a weight of :
 View Solution
View SolutionA boy is standing on a truck moving with a constant velocity of 15m/s on the horizontal road. The boy throws a ball in such a way that it returns to the truck after the truck has moved 60m. Find the speed and the angle of projection (a) as seen by the truck and (b) as seen from the road.
View SolutionIn the figure, a smooth pulley of negligible weight is suspended by a spring balance. Weights of 1 kg and 5kg are attached to the opposite ends of a string passing over the pulley and move with an acceleration due of gravity. During their motion, the spring balance reads a weight of
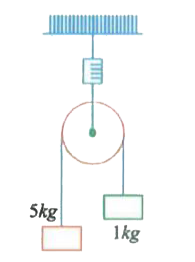 View Solution
View SolutionA block of mass 1kg is kept on smooth floor of a truck. One end of a spring of force constant 100N/m is attached to the block and other end is attached to the body of truck as shown in the figure. At t=0, truck begins to move with constant acceleration 2m/s2. The amplitude of oscillation of block relative to the floor of truck is
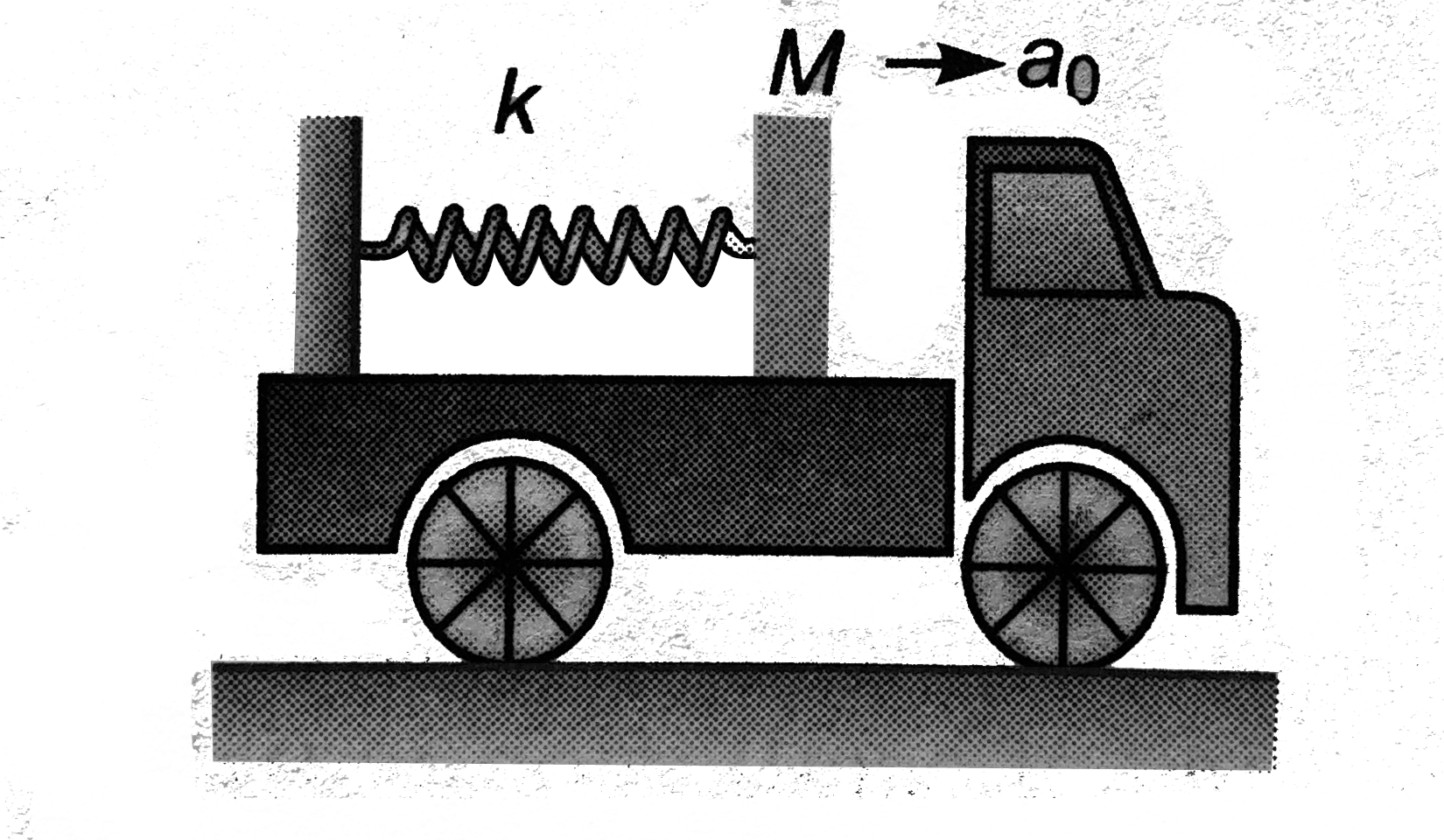 View Solution
View SolutionA smalll bob attached to a string of length l is suspended from a rigid support and rotates with uniform speed along a circle in a horizontal plane. Let θ be the angle made by the string with the vertical, then the length of a simple pendulum having the same period is
View Solution

