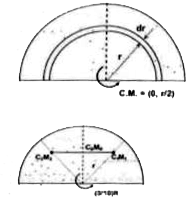
Find the position of centre of mass of the quarter solid sphere from 'C' in which mass per unit volume is given as $ρ (r) = ρ_{0} (1 - \frac{r}{R})$ , where r is radial distance from centre and R is radius of solid quarter sphere

$\frac{3}{10} R$

$\frac{3 \sqrt{2}}{7} R$

$\frac{3 \sqrt{2}}{10} R$

$\frac{3 \sqrt{2}}{5} R$

Text Solution

Verified by Experts

$y_{c m} = \frac{\int_{0}^{R} [ρ_{0} (1 - \frac{r}{R}) (2 π r^{2} d r)] \frac{r}{2}}{\int_{0}^{R} ρ_{0} (1 - \frac{r}{R}) (2 π r^{2}) d r}$
$= \frac{\frac{1}{2} (\frac{R^{4}}{4} - \frac{R^{5}}{5 R})}{(\frac{R^{3}}{3} - \frac{R^{4}}{4 R})} = \frac{12}{2} . \frac{R}{20} = \frac{3}{10} R$
Position of C.M. from C
$= (\frac{3 \sqrt{2}}{10} R)$

Updated on:21/07/2023

Charge density of a sphere of radius $R$ is $ρ = \frac{ρ_{0}}{r}$ where r is distance from centre of sphere.Total charge of sphere will be

A $ρ π e R^{2}$
B $2 ρ_{0} π e R^{2}$
C $3 ρ_{0} π e R^{2}$
D $4 ρ_{0} π e R^{2}$
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density $ρ = \frac{A}{r}$ , where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
A $\frac{A R}{8 ε_{0}}$
B $\frac{A R}{4 ε_{0}}$
C $\frac{A R}{ε_{0}}$
D $\frac{A R}{2 ε_{0}}$