A body of mass 4 kg collides elastically with another body of mass 2 kg at rest. If time of collision is 0.02 sec and average impulse force acted on each body is 100N, find the velocity of 4kg body before and after collision (Assuming collision takes place on a smooth horizontal surface)
To solve the problem step by step, we will use the principles of impulse and momentum, along with the conservation of momentum and the properties of elastic collisions.
Step 1: Understand the given data
- Mass of body 1 (M1) = 4 kg
- Mass of body 2 (M2) = 2 kg
- Initial velocity of body 1 (U1) = V0 (unknown)
- Initial velocity of body 2 (U2) = 0 m/s (at rest)
- Average impulse force (F) = 100 N
- Time of collision (Δt) = 0.02 s
Step 2: Calculate the change in momentum using impulse
Using the impulse-momentum theorem, we know that impulse (J) is equal to the change in momentum (ΔP):
J=F⋅Δt
J=100N⋅0.02s=2Ns
The change in momentum for body 1 (M1) is:
J=M1⋅(V1−V0)
Where V1 is the final velocity of body 1 after the collision.
Step 3: Set up the equation for body 1
From the impulse equation:
2=4⋅(V1−V0)
2=4V1−4V0
Rearranging gives:
4V1−4V0=2
V0−V1=12(Equation 1)
Step 4: Apply conservation of momentum
The total momentum before the collision equals the total momentum after the collision:
M1⋅U1+M2⋅U2=M1⋅V1+M2⋅V2
Substituting the known values:
4V0+2⋅0=4V1+2V2
This simplifies to:
4V0=4V1+2V2(Equation 2)
Step 5: Use the property of elastic collisions
In an elastic collision, the relative velocity of separation is equal to the relative velocity of approach:
V2−V1=V0−0
Thus:
V2−V1=V0(Equation 3)
Step 6: Substitute Equation 3 into Equation 2
From Equation 3, we can express V2 in terms of V0 and V1:
V2=V0+V1
Substituting this into Equation 2:
4V0=4V1+2(V0+V1)
Expanding gives:
4V0=4V1+2V0+2V1
Combining like terms:
4V0−2V0=4V1+2V1
2V0=6V1
Thus:
V0=3V1(Equation 4)
Step 7: Substitute Equation 4 into Equation 1
Now substitute Equation 4 into Equation 1:
3V1−V1=12
This simplifies to:
2V1=12
Thus:
V1=14m/s
Step 8: Find V0 using V1
Using Equation 4:
V0=3V1=3⋅14=34m/s
Final Results
- Initial velocity of the 4 kg body (V0) = 34m/s
- Final velocity of the 4 kg body (V1) = 14m/s
- Mass of body 1 (M1) = 4 kg
- Mass of body 2 (M2) = 2 kg
- Initial velocity of body 1 (U1) = V0 (unknown)
- Initial velocity of body 2 (U2) = 0 m/s (at rest)
- Average impulse force (F) = 100 N
- Time of collision (Δt) = 0.02 s
Using the impulse-momentum theorem, we know that impulse (J) is equal to the change in momentum (ΔP):
J=F⋅Δt
J=100N⋅0.02s=2Ns
J=M1⋅(V1−V0)
Where V1 is the final velocity of body 1 after the collision.
From the impulse equation:
2=4⋅(V1−V0)
2=4V1−4V0
Rearranging gives:
4V1−4V0=2
V0−V1=12(Equation 1)
The total momentum before the collision equals the total momentum after the collision:
M1⋅U1+M2⋅U2=M1⋅V1+M2⋅V2
Substituting the known values:
4V0+2⋅0=4V1+2V2
This simplifies to:
4V0=4V1+2V2(Equation 2)
In an elastic collision, the relative velocity of separation is equal to the relative velocity of approach:
V2−V1=V0−0
Thus:
V2−V1=V0(Equation 3)
From Equation 3, we can express V2 in terms of V0 and V1:
V2=V0+V1
Substituting this into Equation 2:
4V0=4V1+2(V0+V1)
Expanding gives:
4V0=4V1+2V0+2V1
Combining like terms:
4V0−2V0=4V1+2V1
2V0=6V1
Thus:
V0=3V1(Equation 4)
Now substitute Equation 4 into Equation 1:
3V1−V1=12
This simplifies to:
2V1=12
Thus:
V1=14m/s
Using Equation 4:
V0=3V1=3⋅14=34m/s
- Initial velocity of the 4 kg body (V0) = 34m/s
- Final velocity of the 4 kg body (V1) = 14m/s
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE)
18 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE) ASSERTION REASONING TYPE
1 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - (NUMERICAL BASED QUESTIONS)
4 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A body of mass m makes an elastic collision with another identical body at rest. Show that if the collisionis not head on the bodiese to at right to each other after the collision.
View SolutionA force acting on a body of mass 2 kg varies with time as shown in fig . 20 find impulse of the force and final velocity of the body.
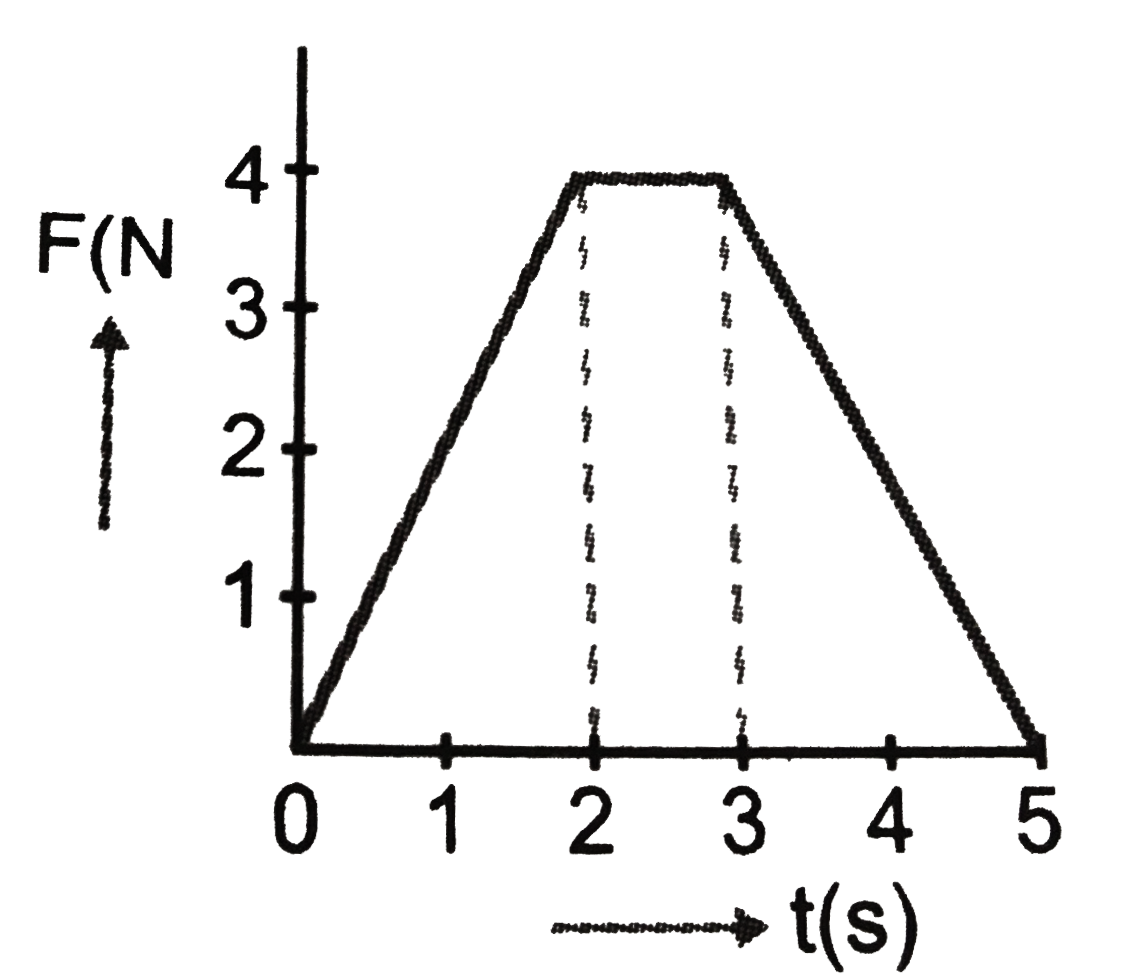
View Solution
Knowledge Check
A body of mass m1 collides elastically with another body of mass m2 at rest. If the velocity of m1 after collision is 23 times its initial velocity, the ratio of their masses is :
A1:5B5:1C5:2D2:5A body of mass M1 collides with another mass M2 at rest. The collision is elastic. Maximum transfer of energy occurs when
AM1=M2BM1>M2CM1<M2DNone of theseA body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
AzeroB288JC172.8JD144J
Body A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View SolutionA body of mass 20gm is moving with a certain velocity. It collides with another body of mass 80gm at rest. The collision is perfectly inelastic. The ratio of the kinetic energies before and after collision of the system is
View SolutionIf a body of mass m collides head on, elastically with velocity u with another identical boday at rest. After collision velocty of the second body will be
View SolutionA body of mass 'm' moving with certain velocity collides with another identical body at rest. If the collision is perfectly elastic and after the collision both the bodies moves
View SolutionBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest, the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View Solution
