Two block of mass 2 kg and M kg are at rest on an inclined plane and are separated by a distance of 6.0 m as a showm in figure. The coefficient of friction between each of the blocks and the inclined plane is 0.25. The 2 kg block is given a velocity of 10.0 m/s up the inclined plans. It collides with M, comes back and has a velocity of 10 m/s when it reaches its initial position. The other block of mass M after the collision moves 0.5 m up and comes to rest. Calculate the coefficient of restitution between the 2 kg block and the mass M.
[Take sinθ≈tanθ=0.5,cosθ=1 and g=10m/sec2]
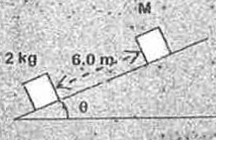
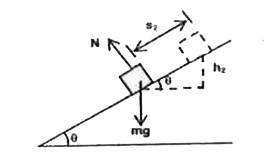
For the block of mass 2 kg (=m) in going from the A to B
(KE+PE)initial=(KE+PE)final+Wfriction
12mv21+0=12mv2f+mgh1+Ffs
of v2f=2[12v2l−gh1−μgs]
Substituting the given data, we get
v2f=2[12(10.0m/s2)−(10m/s2)(0.30m)−(0.25)(10m/s2)(6.0m)]
Or, vf=8m/s
For the block of mass 2 kg (=m) coming back from the position B to A
(KE+PE)initial=(KE+PE)final+Wfriction
12μ2l+mgh1=12μ2f+0+Ffs
u2l=2[12u2f+μgs−ghl]
Substituting the given data, we get
u2l=2[12(−1.0m/s2)+(0.25)(10m/s2)(6.0m)−(10m/s2)(0.30m)]
Or ul=−5.0m/s

For the block of Mass M in going from the position B to C
(KE+PE)initial=(KE+PE)final+Wfriction
12Mc21+Mgh1=12Mc2r+Mg(h1+h2)+FfS2
or 12c21=12c21+gh2+μgs2
12c2i=12(0)+(10m/s2)(0.25m)+(0.25)(10m/s2)(0.5m)
ci=√3m/s
e=ui−civf−ci=(−5.0m/s)−(−√3m/s)(8.0m/s)−0=5+√38=0.84
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Fill in the blanks)
3 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE) MATRIX MATCH TYPE
2 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
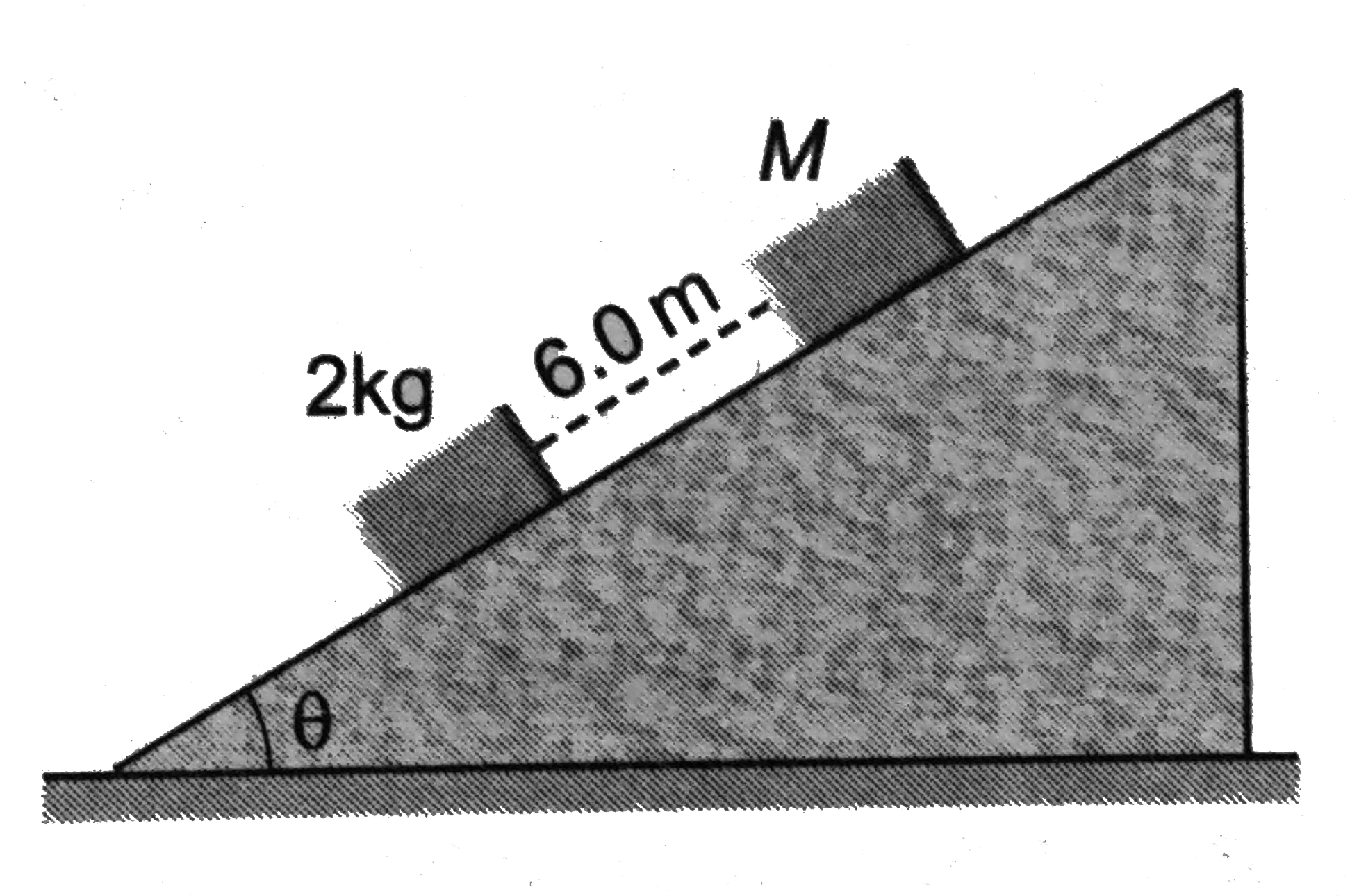
View SolutionTwo blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]

View Solution
Knowledge Check
In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
Two blocks of mass 2 kg and M are at rest as an inclined plane and are sparated of by a distance of 6.0 m as shown in figure . The coefficient of friction between each of the block and the inclined plane is 0.25 . The 2 kg block is given a velocity of 10.0 m//s up the inclined plate if collied with M comes back and has a velocity of 1.0m//s when if rached its inital position , The ofter block M ofter the collisiin its resitition . THe ofter the colition its 0.5 m up and come to rest caleslate the coefficient of resttuion between the block and the mass of the block M [Take sin theta +n tan theta = 0.05anda = 10m//s^(2)]

View SolutionTwo blocks of masses 4 kg and 2 kg are in contact with each other on an inclined plane of inclination 30∘ as shown in the figure . The coefficient of friction between 4 kg mass and the inclined plane is 0.3 , whereas between 2 kg mass and the plane is 0.2 . find the contact force between the blocks .

View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass 0.5 kg has an initial velocity of 10ms−1 down an inclined plane of angle 30∘, the coefficient of friction between the block and the inclined surface is 0.2. The velocity of the block after it travels a distance of 10 m is

View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
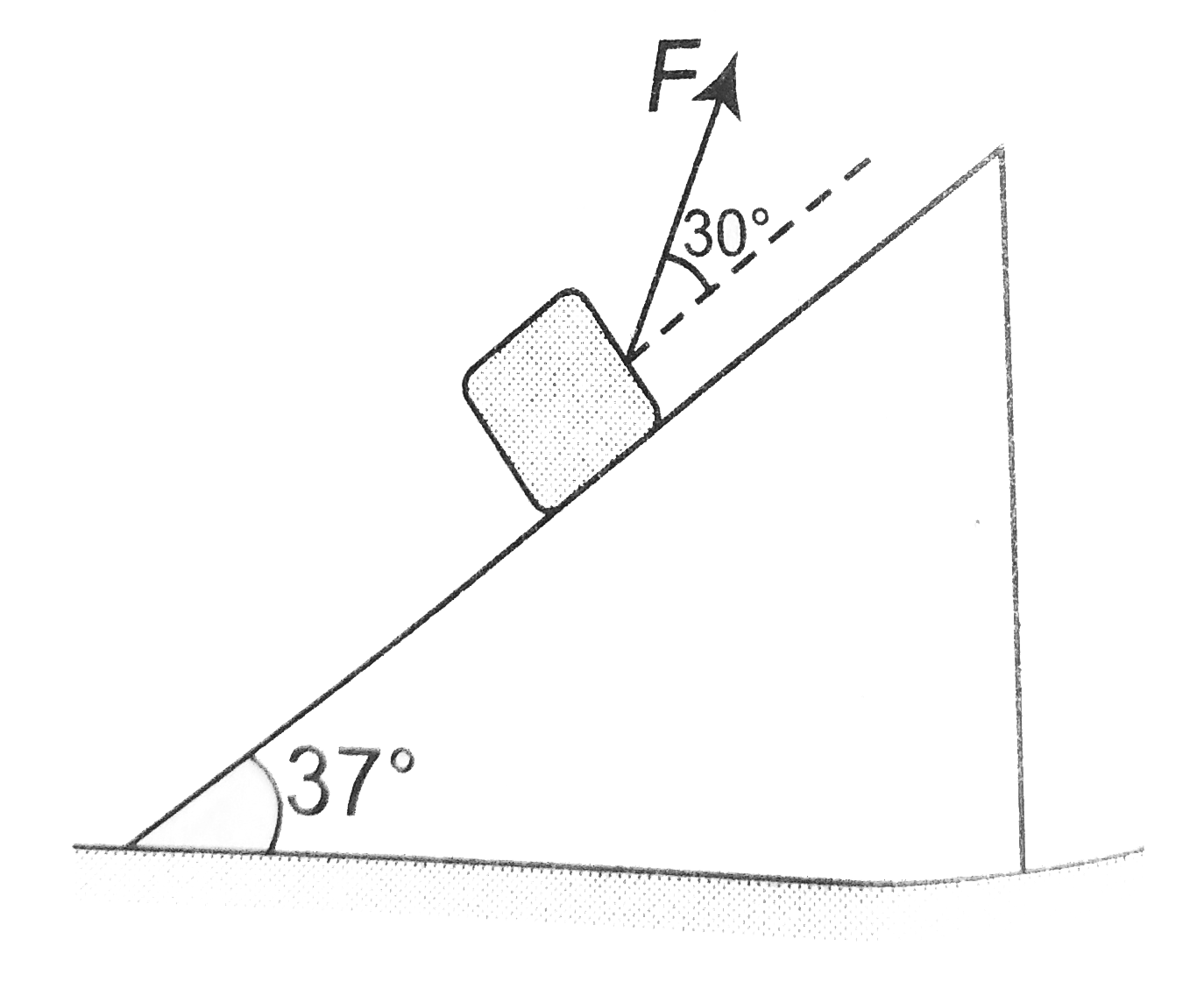
View Solution
