The area of F.t curve is A. If one of the colliding bodies of mass m is at rest, find its speed just after the collision.
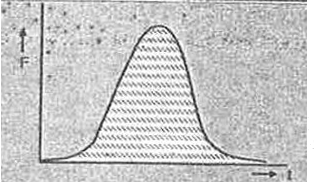
The area of F-t curve gives the impulse of the force F during the time. That is equal to the change in momentum of the colliding bodies. Since one of the colliding body was at rest just before the collision, the change in its momentum during the impacxt is equal to momentum just after the impact, that is mv.
⇒∫Fdt=mv
Since ∫Fdt=A
⇒v=A/m.
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Fill in the blanks)
3 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE) MATRIX MATCH TYPE
2 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View Solution
Knowledge Check
The area of F-t curve is A, where 'F' is the force on one mass due to the other. If one of the colliding bodies of mass M is at rest initially, its speed just after the collision is :
AA/MBM/ACAMD√2AMThe area of F-t curve is A, where 'F' is the force on one mass due to the other. If one of the colliding bodies of mass M is at rest initially, its speed just after the collision is :
AA/MBM/ACAMD√2AMA particle of mass m1 moving with velocity v collides with a mass m2 at rest, then they get embedded. Just after collision, velocity of the system
AincreasesBdecreasesCremains constantDbecomes zero
Body A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View SolutionA body of mass 'm' moving with certain velocity collides with another identical body at rest. If the collision is perfectly elastic and after the collision both the bodies moves
View SolutionBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View SolutionBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest, the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View SolutionBody A of mass 4 m moving with speed u collides with another body B of mass 2m, at rest. The collision is head on and elastic in nature. After the collision the fraction of energy lost by the colliding body A is
View Solution
