A man of mass m climbs a rope of length L suspended below a balloon of mass M. The balloon is stationary with respect to ground. If the man begins to climb up the rope at a speed vrel. (relative to rope) in what direction and with what speed (relative to gound) with the balloon move ?
The change in momentum Δp of the ball during Δ=0.01 sec is known as the impulse (FΔt) of the force of impact
⇒FΔt=Δp
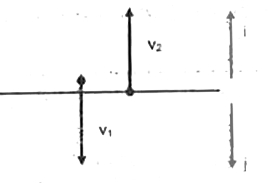
|Δ→p|=|m→v2−m→v1|=m(v1+v2)
∵m→v1&m→v2 are antiparallel
⇒Fδt=m(v1+v2) ...(1)
Since, the ball falls through a height h, and its velocity just before striking the surface is √2gh. As the ball losses 75percent of its total mechanical energy that is knetic energy.
⇒1/2mv22=1/2mv21(1−75/100)
⇒v2=v12=√2gh2=√gh2
Substitution of the values of v1 and v2 in (1) yields
FΔt=50×10−3×3√gh2=50×10−3×3√(9.8)(10)2=1.05 N - sec.
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Fill in the blanks)
3 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE) MATRIX MATCH TYPE
2 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A man of mass m climbs to a rope ladder suspended below a balloon of mass M. The balloon is stationary with respect to the ground.
(a) If the man begins to climb the ladder at speed v (with respect to the ladder), in what direction and with what speed (with respect to the ground) will the balloon move?
(b) What is the state of the motion after the man stops climbing?
View SolutionA man of mass m climbs to a rope ladder suspended below a balloon of mass M. The balloon is stationary with respect to the ground.
(a) If the man begins to climb the ladder at speed v (with respect to the ladder), in what direction and with what speed (with respect to the ground) will the balloon move?
(b) What is the state of the motion after the man stops climbing?
View Solution
Knowledge Check
A man of mass M hanging with a light rope which is connected with a balloon of mass m. the system is at rest in air. When man rises a distance h with respect to balloon find. The distance raised by man
Amhm+MBMhm+MCm+MmhDm+MMh
A man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velocity relative to the ice does the platform recoil?
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionA balloon of mass M is stationary in air. It has a ladder on which a man of mass m is standing. If the man starts climbing up the ladder with a velocity of relative to ladder, the velocity of balloon is
View SolutionA boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View Solution
