Two blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
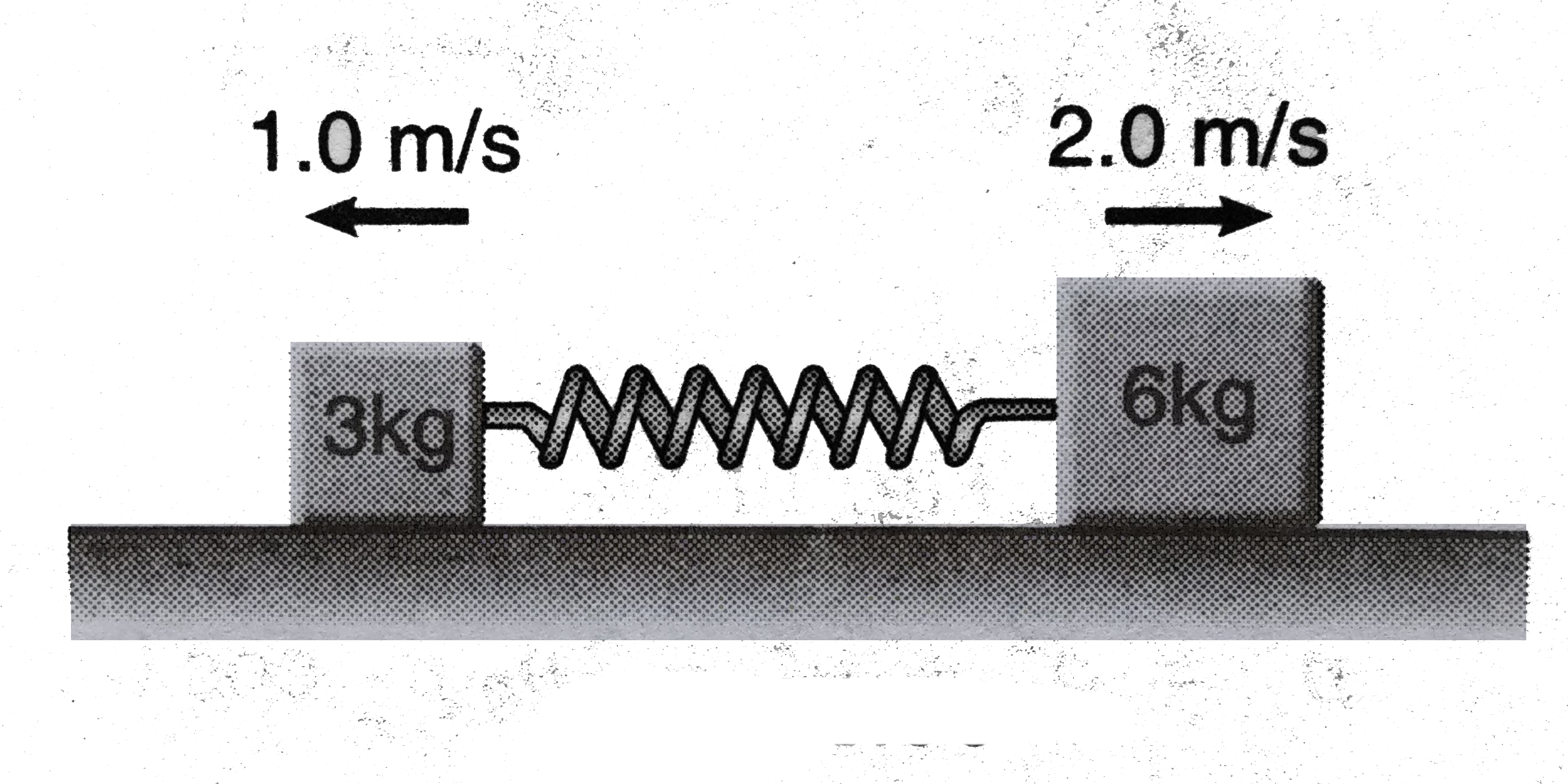
57 cm
25 cm
20 cm
15 cm
The correct Answer is:A
Step by step video, text & image solution for Two blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N//m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II
20 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II
17 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
Two bolcks A & B are connected by a spring of stiffness 512N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. The indicated velocities are imparted to A & B. Find the maximum extension in the spring?
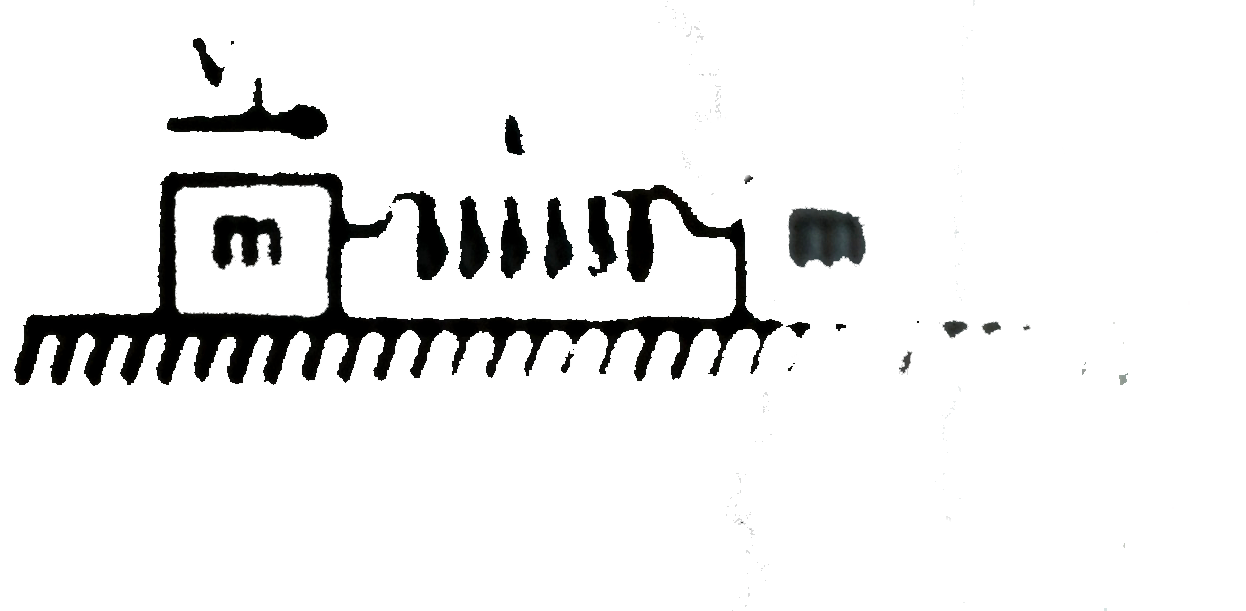
View SolutionTwo blocks A (2 kg) and B (3 kg) rest on a smooth horizontal surface, connected by a spring of stiffness k = 120 N/m. Initially, the spring is relaxed. At t = 0, A is imparted a velocity u = 2 m/s towards right. Find displacement of block A as a function of time.

View Solution
Knowledge Check
Two blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
A110B12√10C12√15D0.15A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
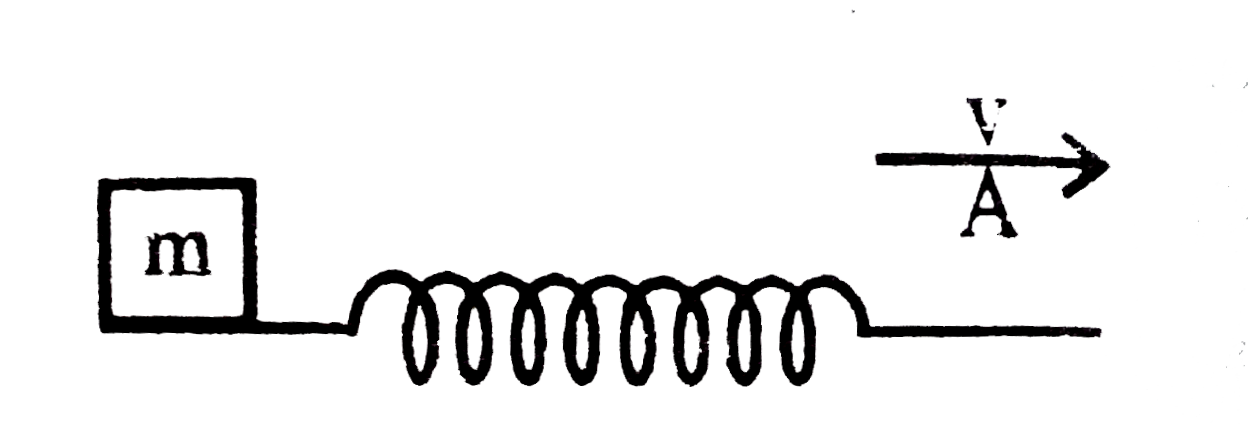 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
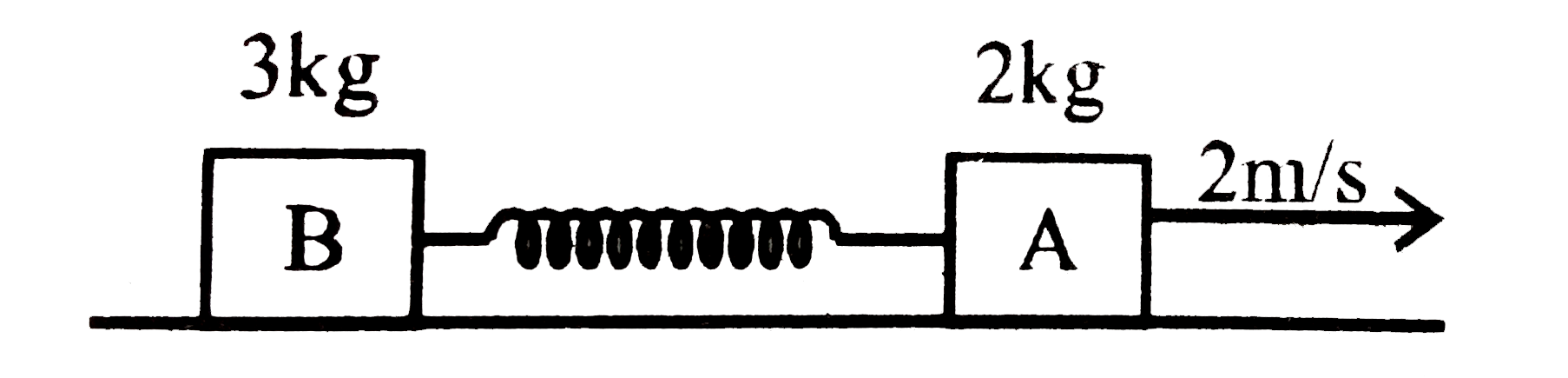
The blockA(2kg) and B(3kg) rest up on a smooth horizontal surface are connected by a spring of stiffness 120N/m. Identially the spring is underformd. A is imparted a velocity of 2m/s along the line of the spring away from B. Find the displacement of A at t seconds later.
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring
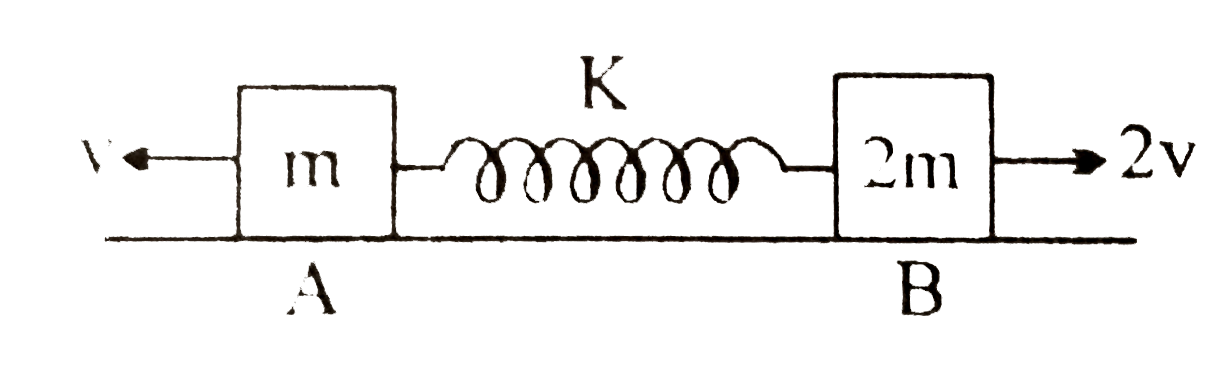
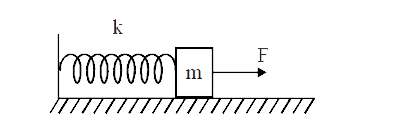
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
maximum extension in the spring
View SolutionTwo blocks A and B of equal mass m=1.0kg are lying on a smooth horizontal surface as shown in figure. A spring of force constant k=200N/m is fixed at one end of block A. Block B collides with block A with velocity v0=2.0m/s. Find the maximum compression of the spring.

View SolutionTwo blocks A(3kg) and B(6kg) are connected by a spring of stiffness 512 N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. Velocities 1.8m/s and 2.2 m/s are imparted to A and B in opposite direction. The maximum extension in the spring will be –
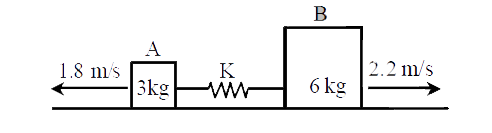
View Solution
