In the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., mK=2π2
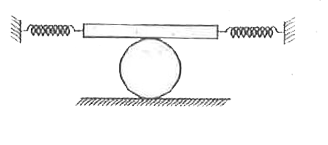
If the plank is displaced slightly by x towards left, then

2Kx−f1=ma2 …(i)
f1+f2=8ma1 …(ii)
τcm=lcmα
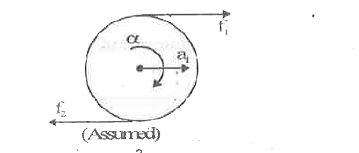
or (f1+f2)R=(8m)R22α
(f1+f2)=(8m)a12 ...(iii)
From (ii) and (iii),
2f1=(8m)×3a12
or f1=(8m)×3a14
and f2=−2ma1
Hence f2 will be in forward direction.
Also, for no slipping, at the point of contant between plank and cylinder
2a1=a2 ...(iv)
f1=(8m)×(3a28)=(3m)a2 ...(v)
from (i) and (v)
2Kx−(3m)a2=ma2
a2=2K4mx
or (−d2xdt2)=(2K4m)x
or d2xdt2=−(24×π22)x
orω2=π24
or ω=π2
or 2πT=π2
or T = 4 seconds.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Subjective)
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
A plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.

View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these osillations.

View Solution
Knowledge Check
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
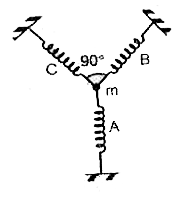 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)A block of mass m is placed in equilibrium on a moving plank. The maximum horizontal acceleration of the plank for μ=0.2 is:
A2m/s2B3m/s2Cdependent on the mass mDnone of theseA body of mass m = 2kg hangs from three springs, each of spring constant 1875 N/m, as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period
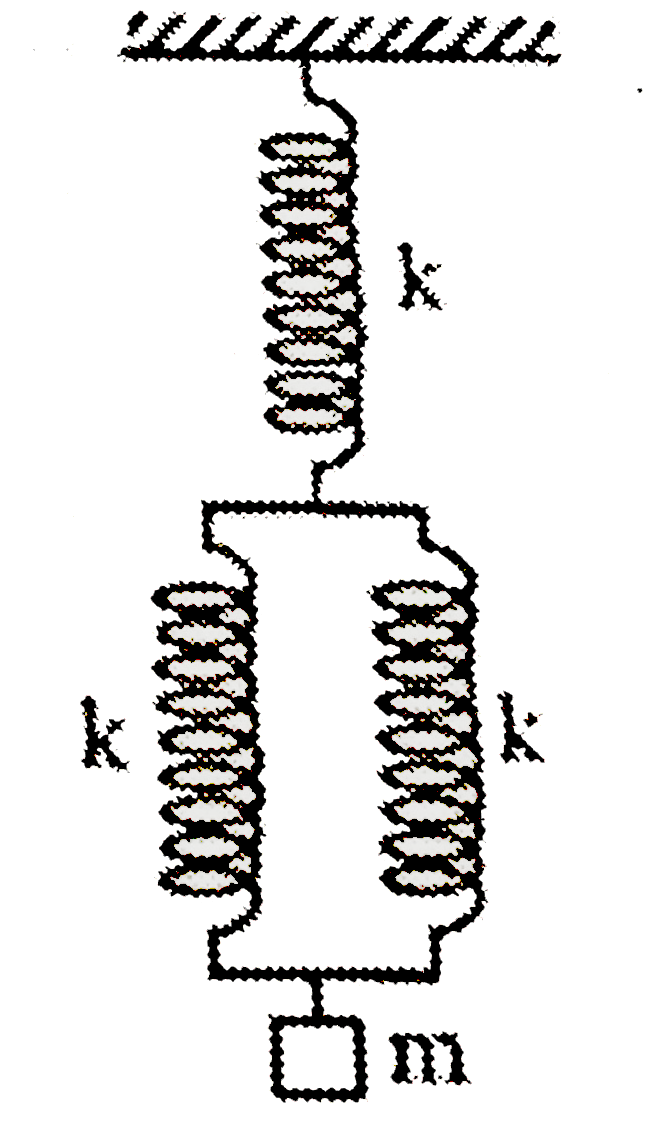 Aπ5 secBπ25 secC2π5secD2π25 sec
Aπ5 secBπ25 secC2π5secD2π25 sec
A solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding.
x
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
x
View SolutionA cylinder of mass 2kg and radius 10cm is held between two planks as shown in Fig. Calculate KE of the cylinder when there is no slipping at any point.

View SolutionA uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
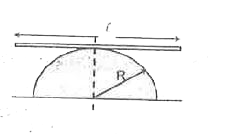
View Solution
