A block of mass 'm' is attached to a spring and is placed on a platform as shown in the figure, and the spring at this stage remains in a relaxed stage. When supporting platform is suddenly removed the mass begins to oscillate and moves down to a lowest position of 5 cm from its initial position. Then calculate the time taken by block to reach a height of 3 cm from its lowest position?

π40+120sin−1(1/5)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-I)
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-I) (Assertion Reasoning type)
Explore 3 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Subjective) (Level)
Explore 20 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
A block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
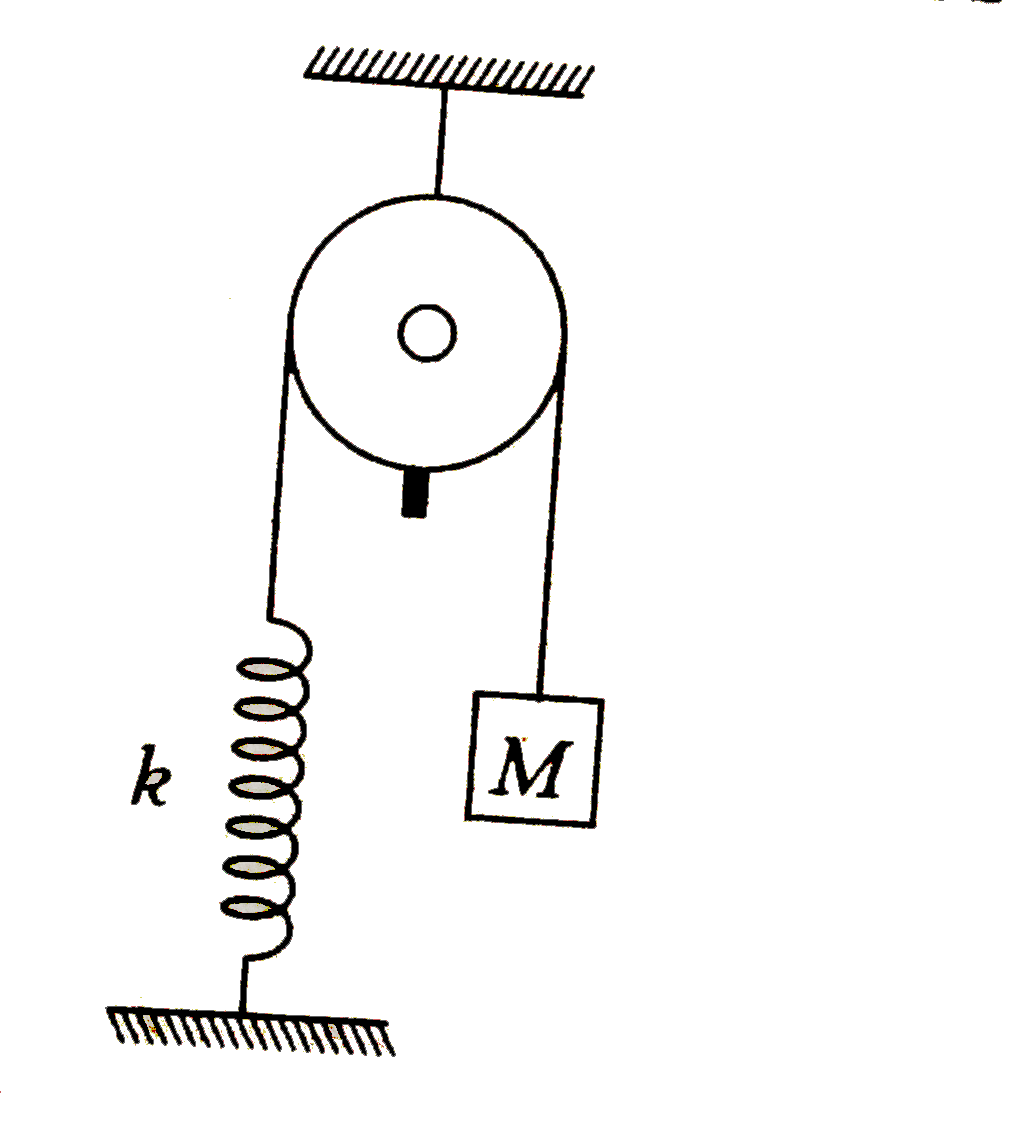
View Solution
Knowledge Check
A block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ⟨h and spring constant = K)-
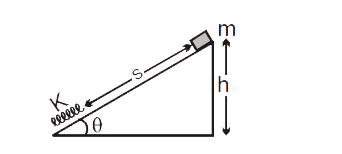 A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh/mK)1/2
A(2mgh/K)1/2B(mgh/K)1/2C(2gh/mK)1/2D(gh/mK)1/2A mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
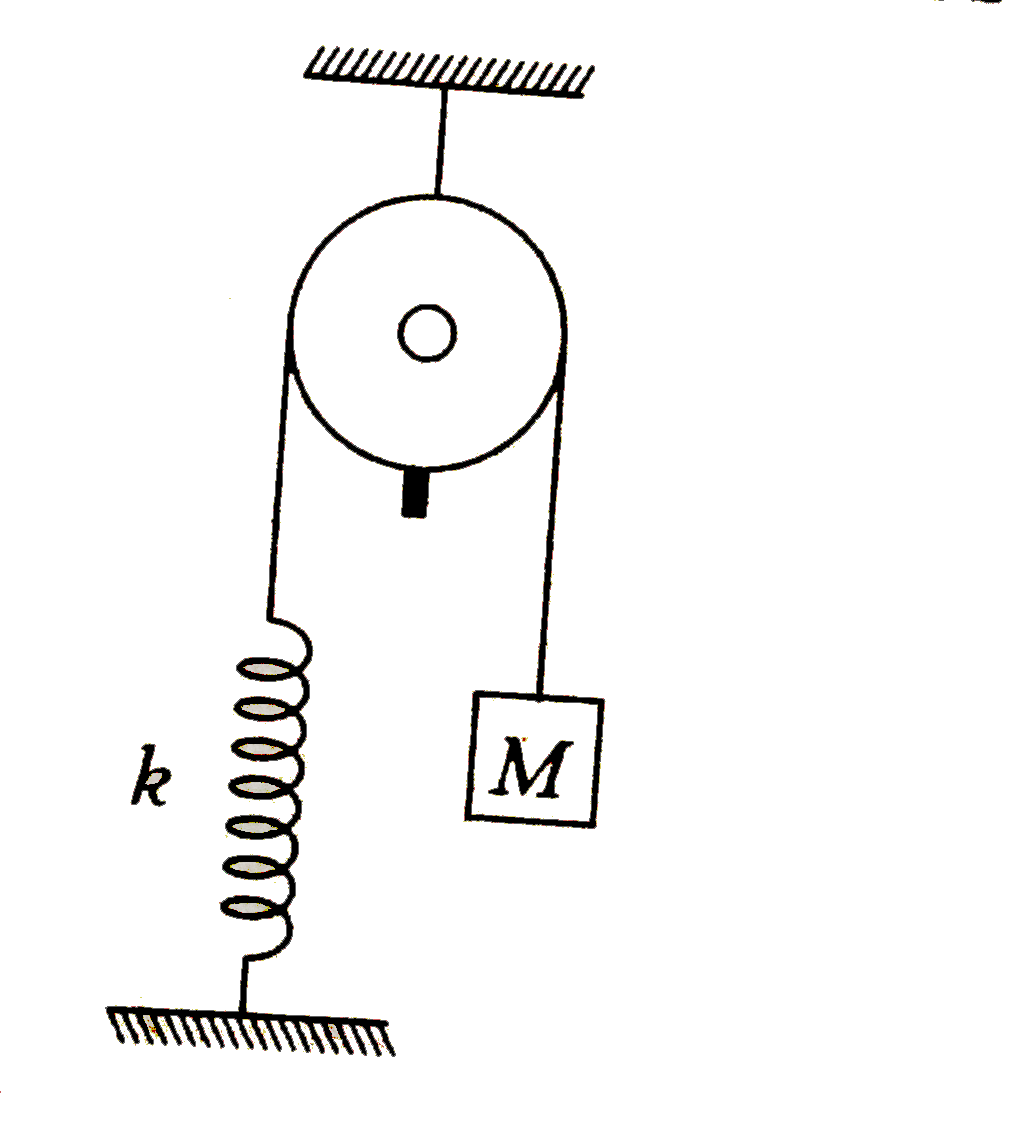 A0.5 mB0.25 mC0.2 mD0.1 m
A0.5 mB0.25 mC0.2 mD0.1 mA ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
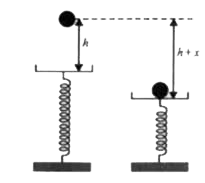 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
A block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View SolutionA block of mass 100g attached to a spring ofstiffness 100N/Mis lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collation with the wall is elastic then find the time period of oscillations.

View SolutionA block of mass m falls from a height h onto the end of a platform as shown in figure. The springis initially unstreched and the mass of the platform on be neglected. Assuming if there is no loss of energy, the maximum elongation of the spring is
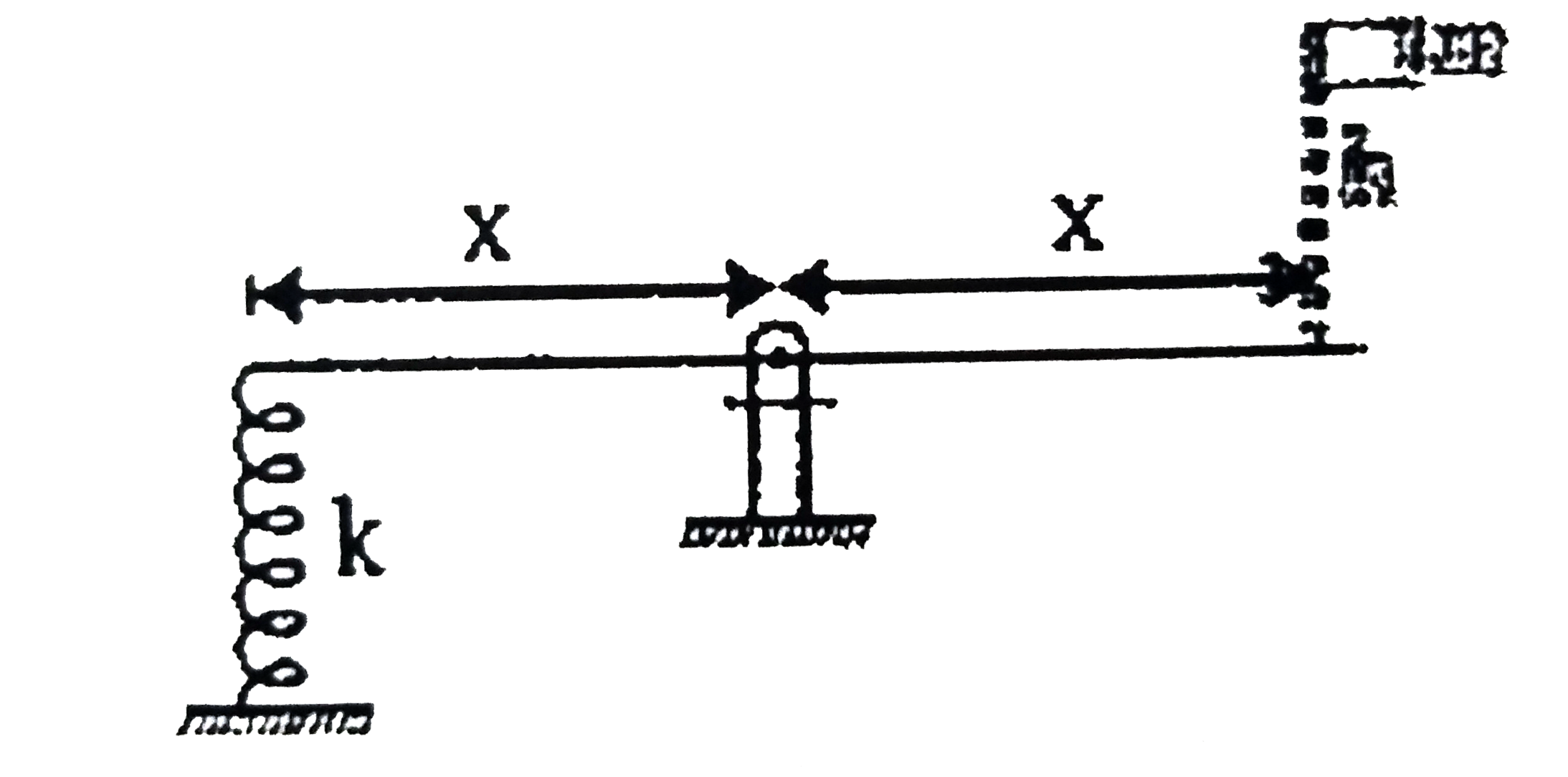
View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View Solution
