A uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-I)
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-I) (Assertion Reasoning type)
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Subjective) (Level)
20 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
A uniform rod of mass 'm' and length 'l' is hinged at one end 'A'. It can rotate freely about a horizontal axis passing through 'A'. If it is given a sloght angular displacement and left to itself then it oscillate. Find the time period of small oscillations.

View SolutionA ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.
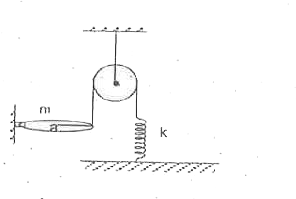
View Solution
Knowledge Check
A uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take π2=10)
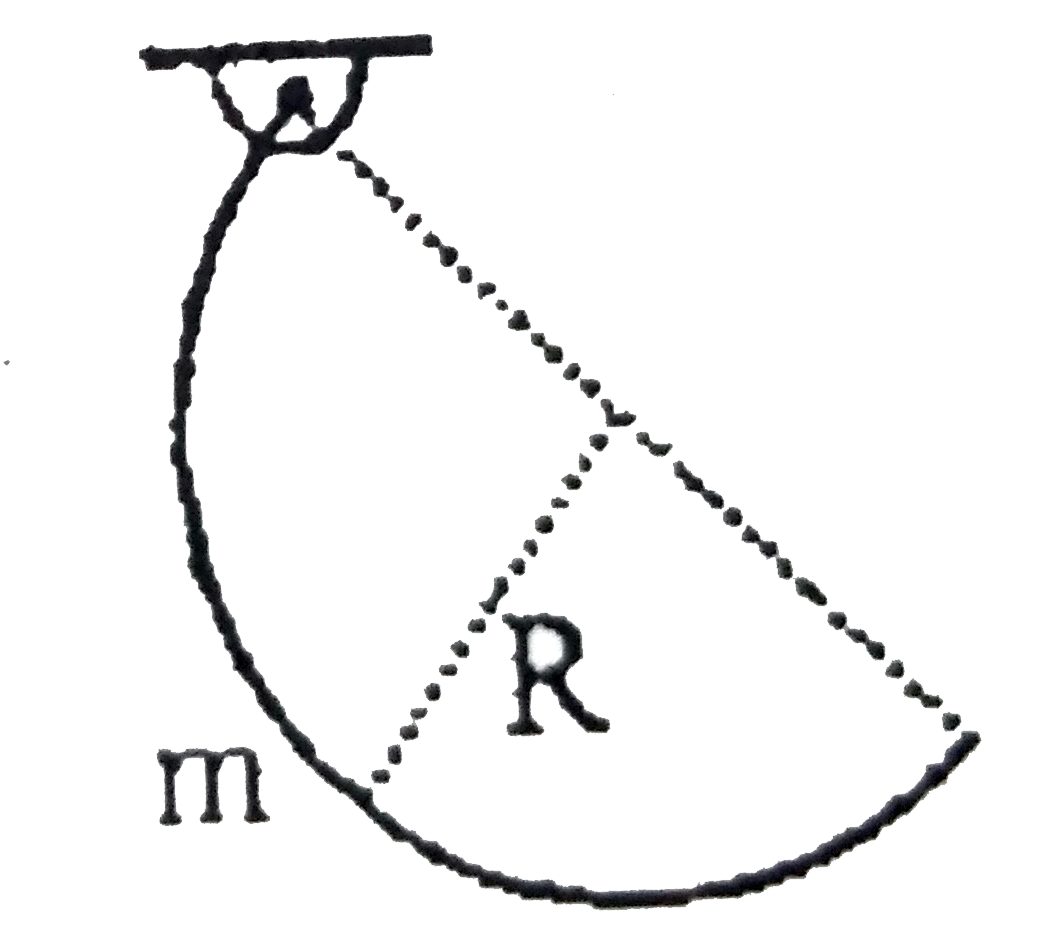 A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)
A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring isA2π ⎷rg(1+1π2)B2π ⎷rg(1+4π2)12C2π ⎷rg(1−2π2)12D2π ⎷2rg(1+4π)12A L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane as shwon. If it is slightly displaced from its equilibrium position then the frequency of oscillation is…….
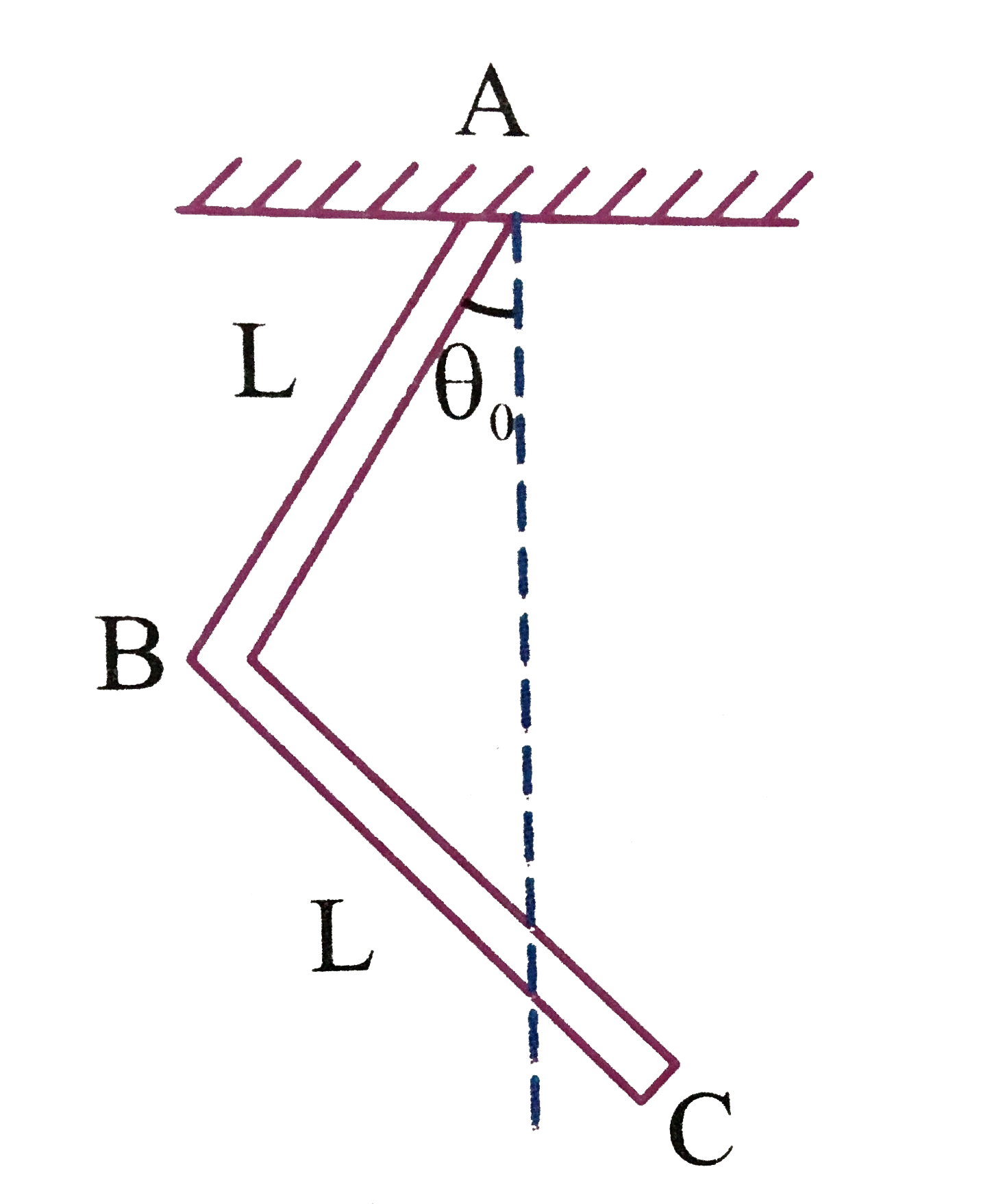 A12π ⎷(gL(3√104)B12π ⎷gL(√104)C12π√gL(√2)D12π√g2L
A12π ⎷(gL(3√104)B12π ⎷gL(√104)C12π√gL(√2)D12π√g2L
A ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.

View SolutionA uniform quarter circular thin rod of mass M and radius R is pivoted at a point B on the floor. It can rotate freely in the vertical plane about B. It is supported by a smooth vertical wall at its other free end A so that it remains at rest. Find the reaction force of wall on the rod.
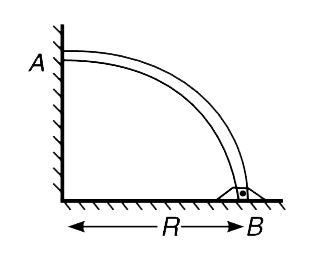
View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. The time period of small oscillations of remaining portion about O is -

View SolutionThe semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
View SolutionThere is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
View Solution
