→B,→H and →I are related according to the equation
A
→B=μ0(→H×→I)
B
∣∣→B∣∣=∣∣→I∣∣∣∣→H∣∣
C
→B=μ0(→H−→I)
D
→B=μ0(→H+→I)
Text Solution
The correct Answer is:D
|
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - FIITJEECHAPTER - MAGNETISM AND MATTEREXERCISE - ASSIGNMENT PROBLEMS OBJECTIVE : (LEVEL -II) (MULTI CHOICE SINGLE CORRECT)
20 Videos
- MAGNETISM AND MATTERBOOK - FIITJEECHAPTER - MAGNETISM AND MATTEREXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) (LEVEL -1)
18 Videos
- MAGNETISMBOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example
12 Videos
- MODERN PHYSICSBOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Numerical based questions
5 Videos
Similar Questions
Knowledge Check
If →A,→B and →C are three vectors, then the wrong relation is :
A→A+(→B+→C)=(→A+→B)+→CB→A.(→B+→C)=(→A.→B)+→A.→CC→A×(→B+→C)=→A×→B+→A×→CD(→A×→B).→C=→A×→B.→CThe vectors →a,→band→c are related by →c=→a+→b . Which diagram below illustrates this relationship ?
A B
B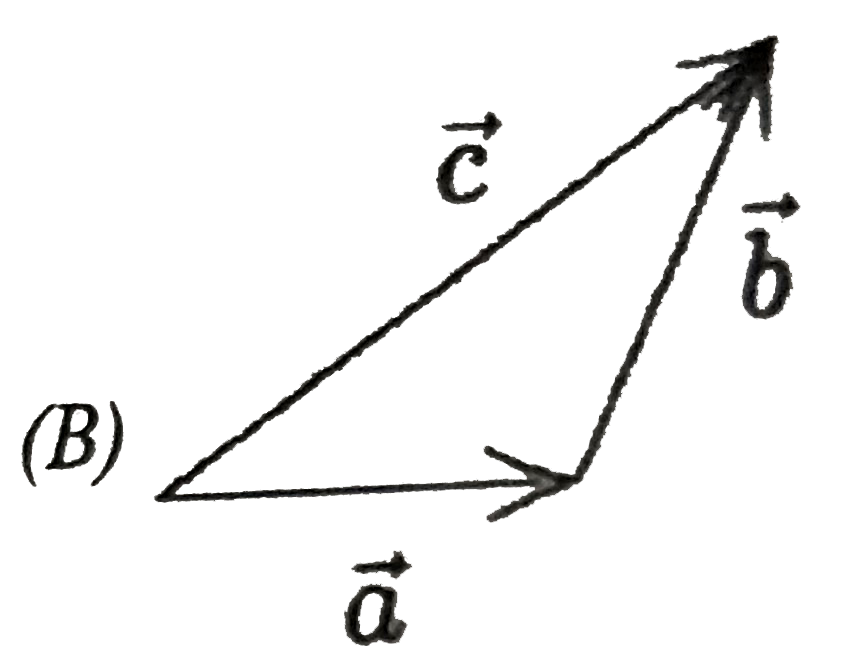 C
C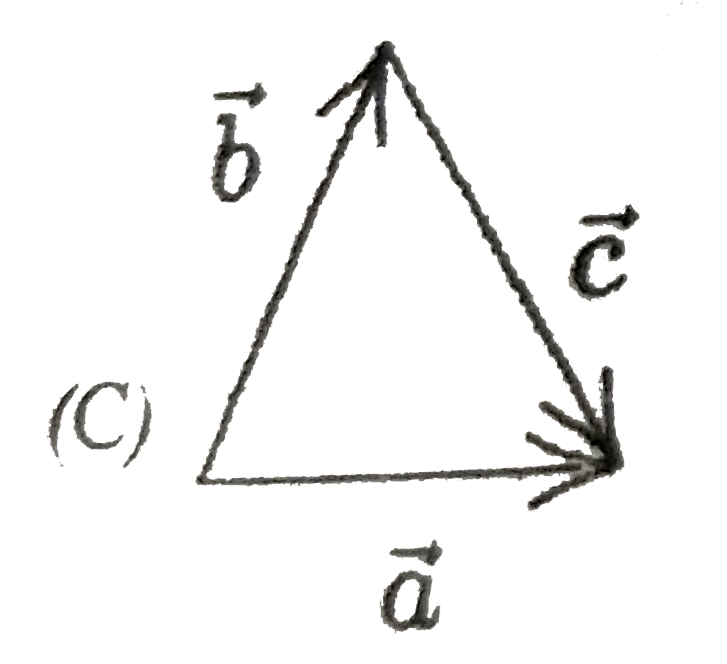 D
D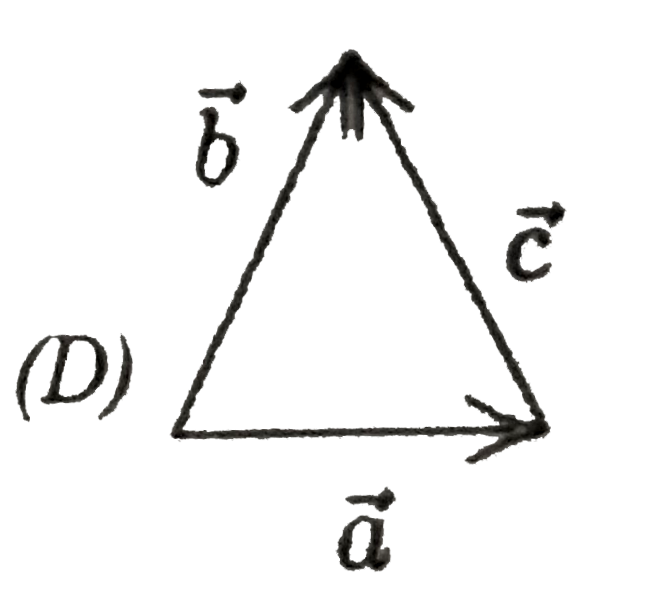
Three vector →A,→B, →C satisfy the relation →A⋅→B=0and →A.→C=0. The vector →A is parallel to
A→BB→CC→B.→CD→B×→C
If →Aand→B are two vectors satisfying the relation →A⋅→B=∣∣→A×→B∣∣. Then the value of ∣∣→A−→B∣∣ will be :
View SolutionGiven below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
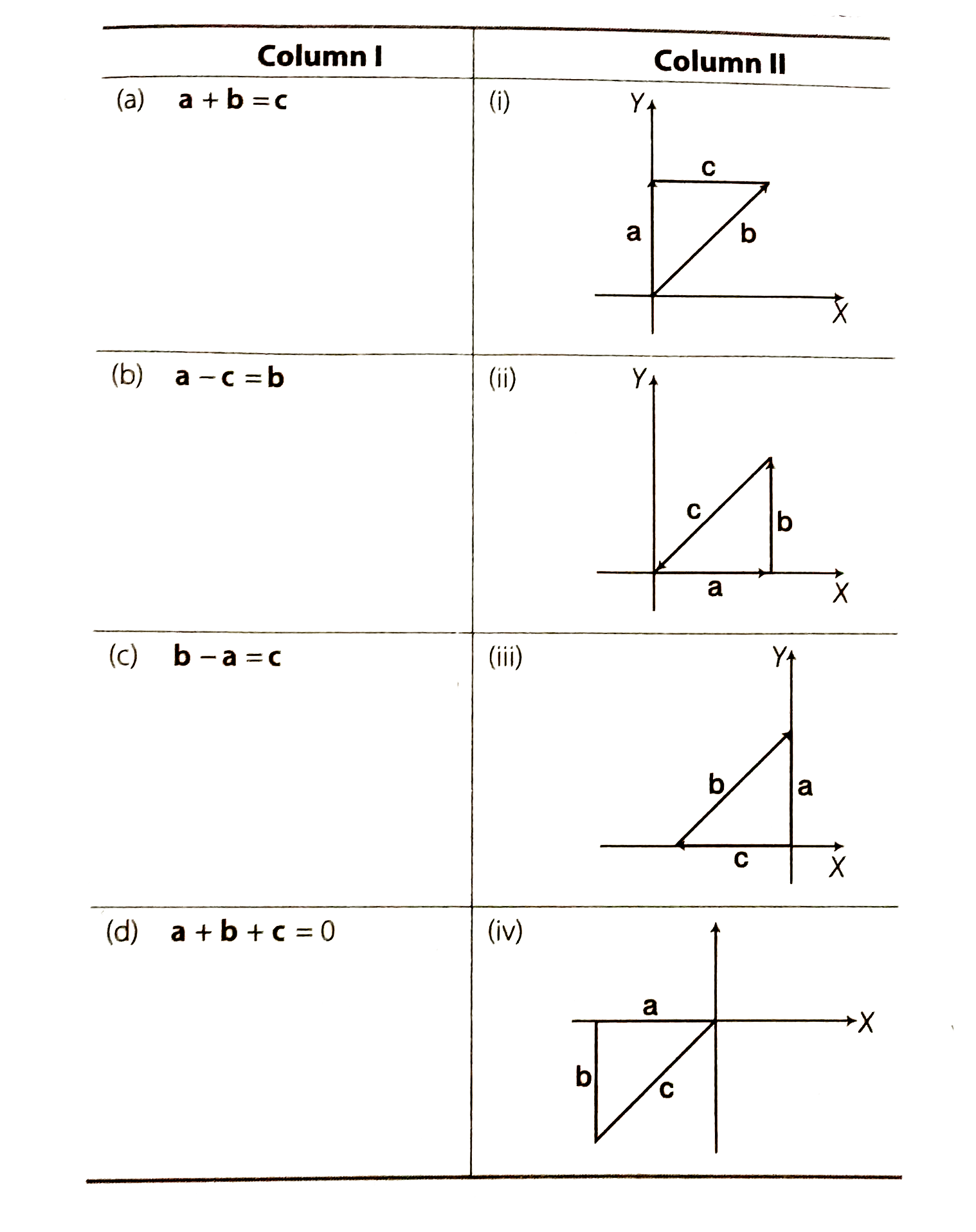
View SolutionThe non-zero vectors are →a,→band→c are related by →a=8→band→c=−7→b. Then the angle between →aand→c is
View SolutionThe non-zero vectors are →a,→band→c are related by →a=8→band→c=−7→b. Then the angle between →aand→c is
View SolutionThe nonzero verctors →a , →b and →c are related by →a=8→b and →c=−7→b . Then the angle between →a and →c is
View Solution
