A metallic rod of length l & resistance R is free to rotate about one of its ends over a smooth rigid circular metallic frame of radius i in an inward magnetic field of induction B. What torque should be applied by an external angent to rotate the rod with constant angular velocity ω ?
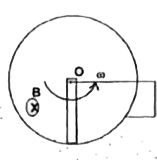
The correct Answer is:B2l4ω4R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE ) LEVEL -I
28 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL -I
1 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT PROBLEMS ( SUBJECTIVE ) Level -I True and False
5 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II
15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTION AND AC CURRENTEXERCISE - Example
15 Videos
Similar Questions
A copper rod AB-of length / pivoted at one end A, rotates at constant angular velocity ω, at right angles to a uniformn magnetic field of induction B. The emf, developed between the mid point of the rod and end B is
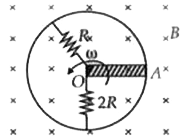
View SolutionA metallic rod of mass m length R is pivoted at O. It is free to rotate about a horizontal axis passing through O . An inward magnetic field is applied as shown in the figure. Find the ratio of maximum electric field inside the metallic rod to the applied magnetic field induction .

View Solution
Knowledge Check
A bent rod PQR with PQ=QR=1 shown in figure-5.329 is rotating about its end P with a constant angular speed ω in a region of transverse magnetic field of induction B:
 AEMF induced across the rod is Bωl2/2BEMF induced across the rod is Bω2l/2CPotential difference between points Q and R on the rod is Bω2/2DPotential difference between points Q and R on the rod is zero
AEMF induced across the rod is Bωl2/2BEMF induced across the rod is Bω2l/2CPotential difference between points Q and R on the rod is Bω2/2DPotential difference between points Q and R on the rod is zeroA copper rod AB of length L, pivoted at one end A, rotates at constant angular velocity omega, at right angles to a uniform magnetic field of induction B. The e.m.f developed between the mid point C of the rod and B is
 ABωl24BBωl22C3Bωl24D3Bωl28
ABωl24BBωl22C3Bωl24D3Bωl28A metallic rod of length L rotates at an angular speed ω, normal to a uniform magnetic field. If the resitance of rod is R the heat dissipated is:
A14B2L4ω2tRB12B2L2ωtRC14B2L2ω2t2RD14BL2ω4tR
A metallic rod of mass m length R is pivoted at O. It is free to rotate about a horizontal axis passing through O . An inward magnetic field is applied as shown in the figure. Find the ratio of maximum electric field inside the metallic rod to the applied magnetic field induction .

View SolutionShows a conducting circular loop radius a placed in a uniform, perpendicular magnetic field B. A metal rod OA is pivoted at the centre O of the loop. The other A of the rod touches the loop. The rod OA and the loop are resistanceless but a resistor having a resistance R is connected between O and a fixed point C on the loop . the rod OA is made to rotate anticlockwise at a small but uniform angular speed omega by an external force. Find (a) the current in the resistance R and (b) the torque of the external force needed ot keep the rod rotating with the constant angular velocity omega.

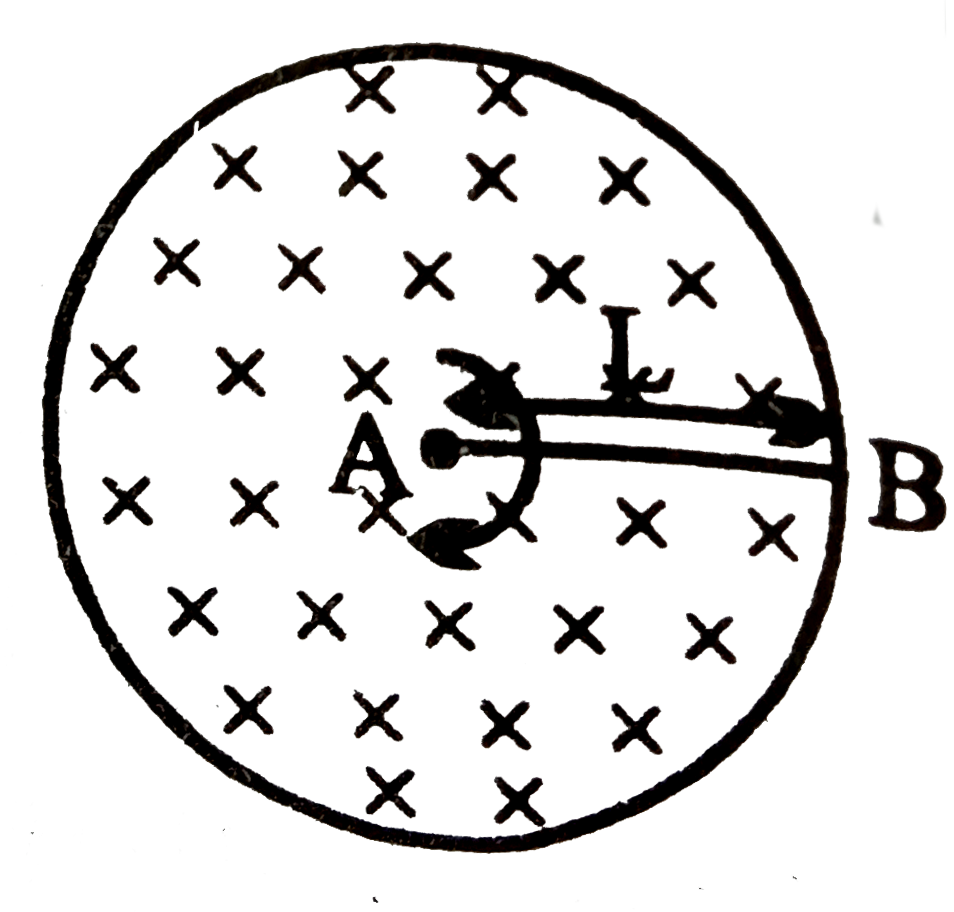
View SolutionA metal rod of mass m can rotate about a horizontal axis O, sliding along a circular conductor of radius a (fig). The arrangment is located in a unifrom magnetic field of induction B directed perpendicular to the ring plane. The axis and the ring are connected to an emf source to form a circuit of resistance R. Neglecting the friction, circuit induction and ring resistance, find the law according to which the source and must very to make the rod rotate with a constant angular velocity ω.
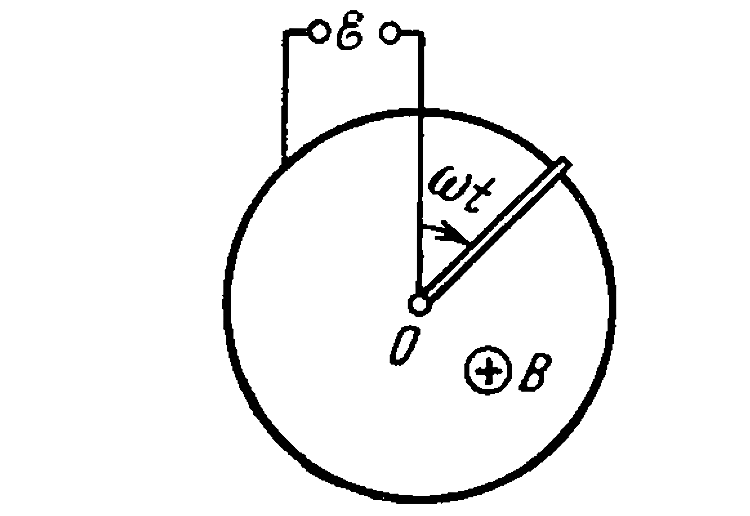
View SolutionA rod OA of length l is rotating (about end O) over a conducting ring in crossed magnetic field B with constant angular velocity ω as shown in figure.
View SolutionA copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
View Solution
