మధ్యగతం =L+n2−cffXh లో cf అనగా
l
f
h
cf
Step by step video solution for మధ్యగతం =L + (n/2 -cf)/f X h లో cf అనగా by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సాంఖ్యకశాస్తంEXERCISE - Exercise147videos
సాంఖ్యకశాస్తం
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సరూప త్రిభుజాలుEXERCISE - Exercise211videos
సరూప త్రిభుజాలు
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - ్రేఢులుEXERCISE - Exercise327videos
్రేఢులు
Similar Questions
ఒక' గ్రామంలో కొంతమంది విద్యార్థుల జట్టు “పర్యావరణ పరిరక్షణ - అవగాహని అనే కార్యక్రమంలో భాగంగా, 20 ఇండ్లలో సర్వే నిర్వహించి, ఎన్నెన్ని మొక్కలు నాటినారో సమాచారాన్ని సేకరించి, ఈ క్రింది పట్టికలో నమోదు చేసినారు. సగటున ఒక ఇంటికి ఎన్ని మొక్కలు నాటినారో కనుక్కోండి.
 12:50View Solution
12:50View Solutionఇచ్చిన పటంలో, DE∣∣AC మరియు DF∣∣AE అయిన BF /FE = BE/ EC అని చూపండి.
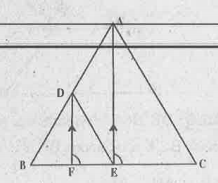 03:35View Solution
03:35View Solutionఒక టాక్సీ మొదటి కి.మీ. ప్రయాణానికి Rs.20 ల చొప్పున, తరువాత ప్రతి కి,మీ.కు Rs.8 ల చొప్పున చెల్లించవలసిన, 15 కి.మీ. ప్రయాణానికి అయ్యే సొమ్ము Rs.....
04:12View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
05:52View SolutionLet f(x) be a differentiable and let c a be a constant. Then cf(x) is also differentiable such that ddx{cf(x)}=cddx(f(x)).
View SolutionIf f is a continuous function on [0,1], differentiable in (0, 1) such that f(1)=0, then there exists some c∈(0,1) such that cf′(c)−f(c)=0 cf′(c)+cf(c)=0 f′(c)−cf(c)=0 cf′(c)+f(c)=0
04:05View SolutionTheorem :(i)Differentiation of a constant function is 0 (ii) Let f(x) be the differentiable function and let c be a constant . Then cf(x) is also differentiable such that dcf(x)dx=c.d(f(x)dx)
01:54View SolutionCF is the internal bisector of angle C of ∠ABC, then CF is equal to
02:12View SolutionIf AD, BE and CF are the medians of a ABC ,then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View Solutionl+(n2−cff)×h सूत्र है:
02:42View Solutionమధ్యగతం =L+n2−cffXh లో cf అనగా
03:47View SolutionIn the given data if N= 230, l = 40, cf = 76, h= 10, f= 65 , then its median is -
02:25View SolutionIf f is a continuous function on [0,1], differentiable in (0, 1) such that f(1)=0, then there exists some c∈(0,1) such that cf′(c)−f(c)=0 cf′(c)+cf(c)=0 f′(c)−cf(c)=0 cf′(c)+f(c)=0
02:40View SolutionLet f(x) be a differentiable and let c a be a constant. Then cf(x) is also differentiable such that ddx{cf(x)}=cddx(f(x)).
03:07View Solutionआकृति में BE⊥CAऔरCF⊥BAजबकिBE=CF तो, निम्न में कौन सत्य है?
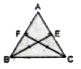 05:40View Solution
05:40View SolutionIf f'(c) is the -derivative of f(x) at x= c,then show that limx→cxf(c)−cf(x)x−c=f(c)−cf'(c)
07:04View Solution

