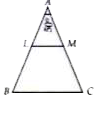
In the given figure (not to scale), ABC is an isosceles triangle in which AB=AC. AEDC is a parallelogram. If ∠CDF=70∘ and ∠BFE=180∘, then find ∠FBA.
A
30∘
B
40∘
C
50∘
D
80∘
Video Solution
Text Solution
i) In a parallelogram, any pair of adjacent angles are supplementary.
ii) ∠EFG=∠FGC=∠AGB and ∠ACB
=∠ABC=∠CDE.(∴∠¯¯¯¯¯¯AC∣∣¯¯¯¯¯¯DE)
iii) Use the above data and find ∠BAC, and then ∠ABC.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - TEST YOUR CONCEPTS29videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS18videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 39videos
COORDINATE GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 310videos
LINEAR EQUATIONS AND INEQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ABC is an isosceles triangle in which AB=ACand∠ABC=50∘,∠BDC :
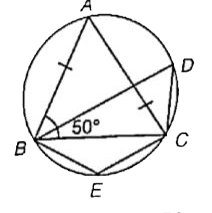A80∘B60∘C65∘D100∘ - Question 2 - Select One
In the given figure, △ABC is an isosceles triangle in which AB=AC and ∠ABC=50∘ , the ∠BDC is equal to
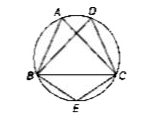A60∘B10∘C80∘D90∘ - Question 3 - Select One
In the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ?
A4 cmB6 cmC7 cmD5 cm
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
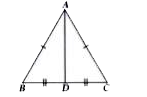Prove that:
∠BAD=∠CADView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
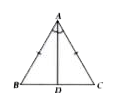
∠B=∠CView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
BD = CDView SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
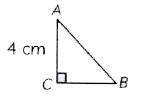View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
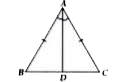
AD⊥BCView Solution