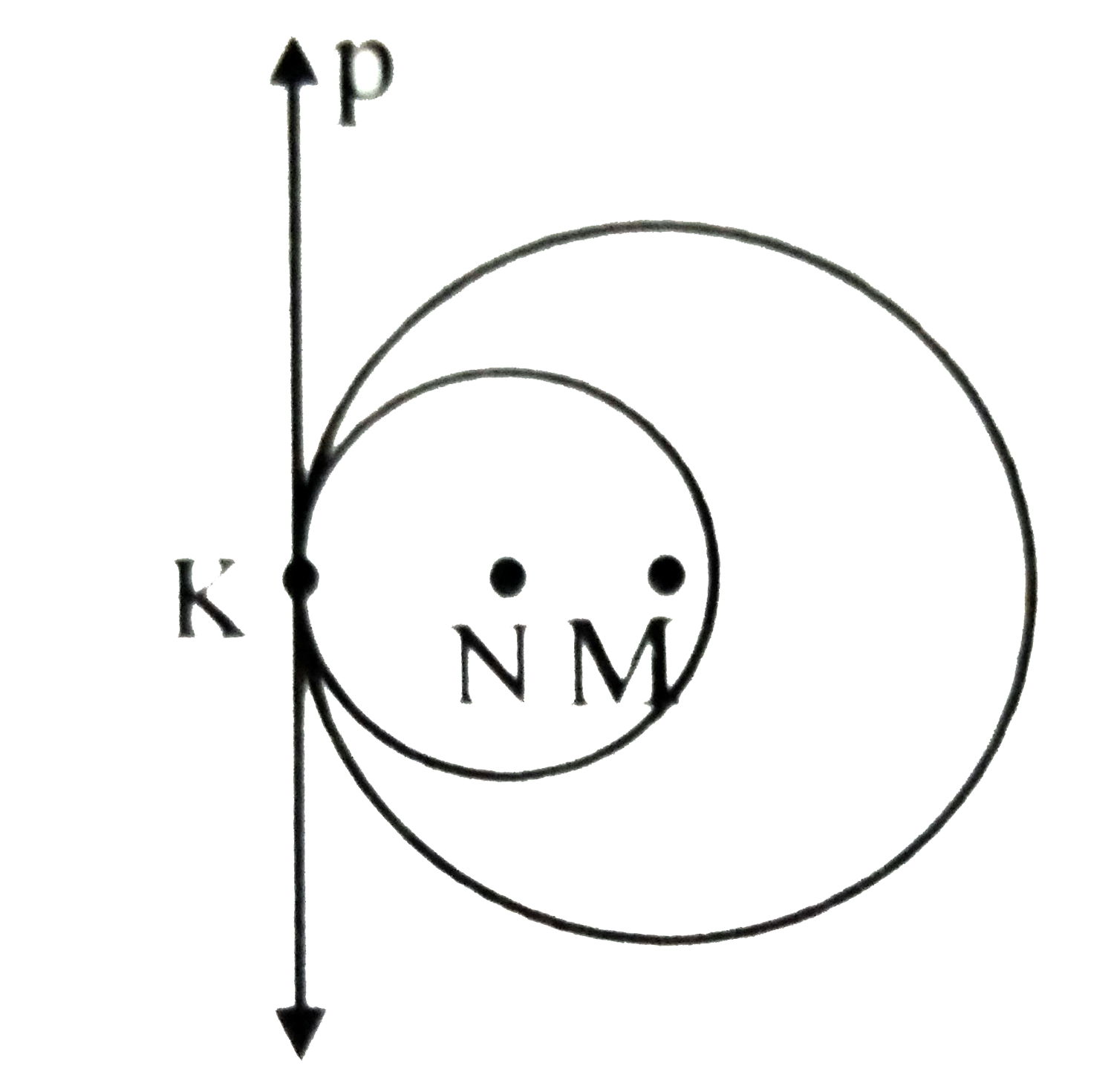
A and B are the centers of the circles as shown in the given figure. The circles interect at C and D. Find ∠CED+∠CFD.

90∘
135∘
120∘
150∘
i) Join AB, which is the radius of both the circles.
ii) AC=AD=BD=BD= radius.
iii) △ABC and △ABD are equilateral triangles. ∠CAD=∠BAD=120∘.
iv) ∠CED=∠CFD=12∠CAD=12∠CBD.
(Angle at the centers is equal to half the angle at the circumference).
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - TEST YOUR CONCEPTS
29 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Knowledge Check
In the figure, O is the center of the circle. What is average of the numbers a, b, c and d?
 A45B60C90D180
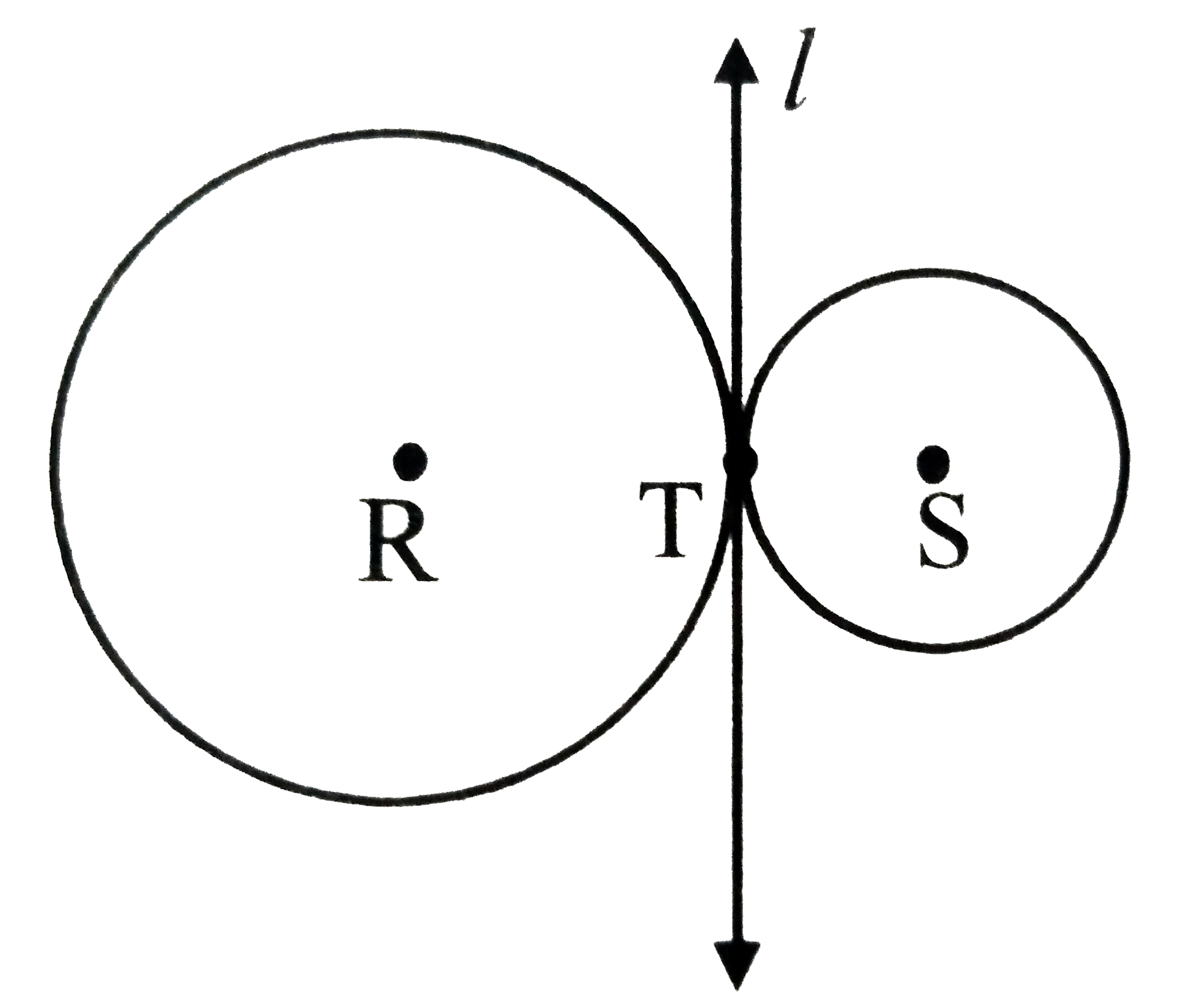
A45B60C90D180A and B are centers of two circles that touch each other externally, as shown in the figure.What is the area of the circle whose diameter is AB?
 A4πB25π/4C9πD16π
A4πB25π/4C9πD16π
In Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
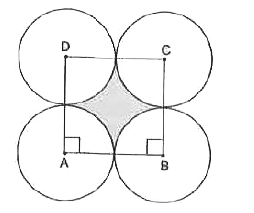
View SolutionIn the given figure, four equal circles are described about corners of a square so that each circle touches two of the circles as shown in the figure. Find the area of the shaded region, each side of the square measuring 14 cm.
View SolutionIf O is the center of the circle, find the value of x in each of the following figures:
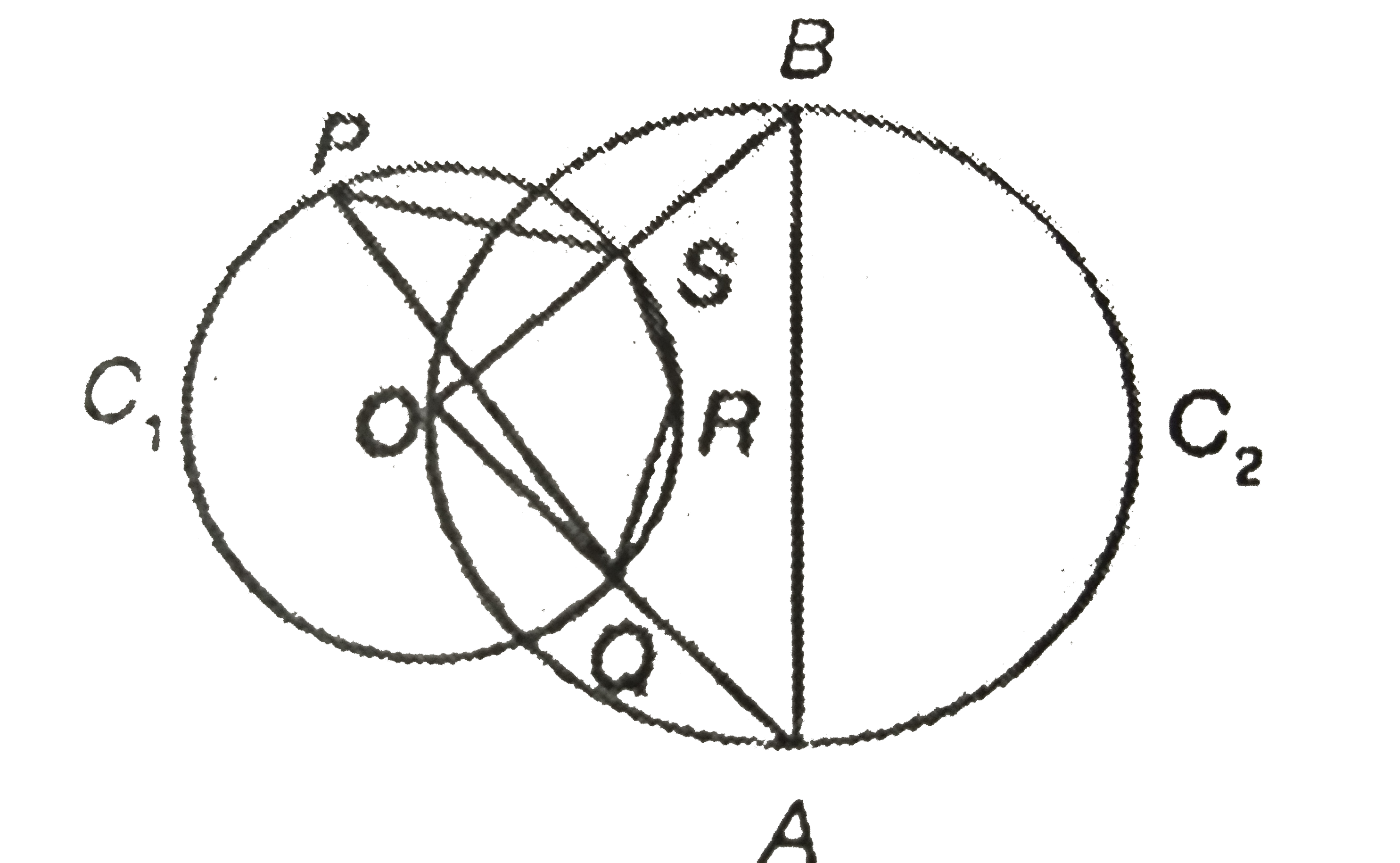
View SolutionIn the given figure (not to scale), O is the center of the circle C1 and AB is the diameter of the circle C2. Quadrilateral PQRS is inscribed in the circle with center O. Find ∠QRS.
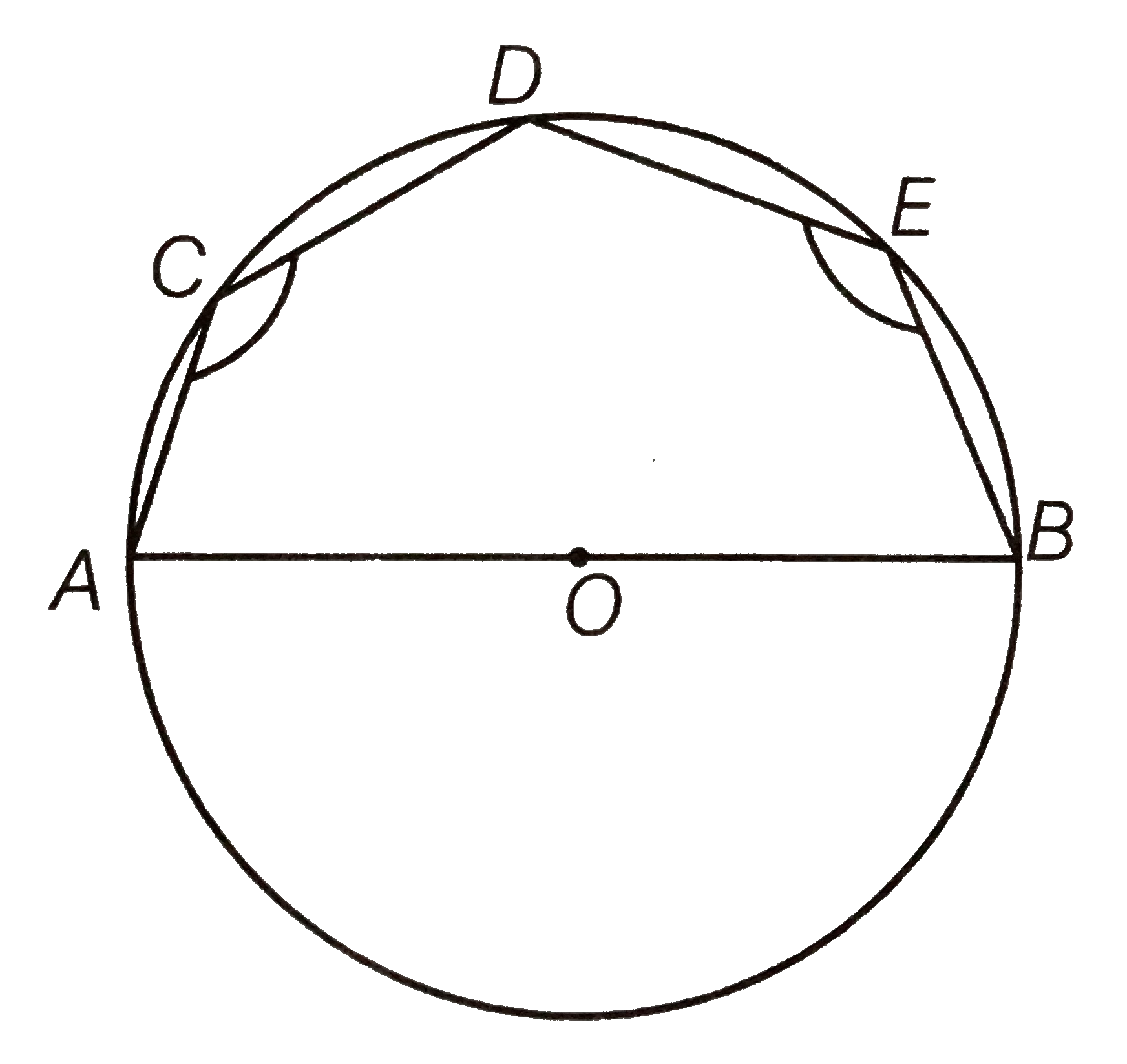
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
View Solution