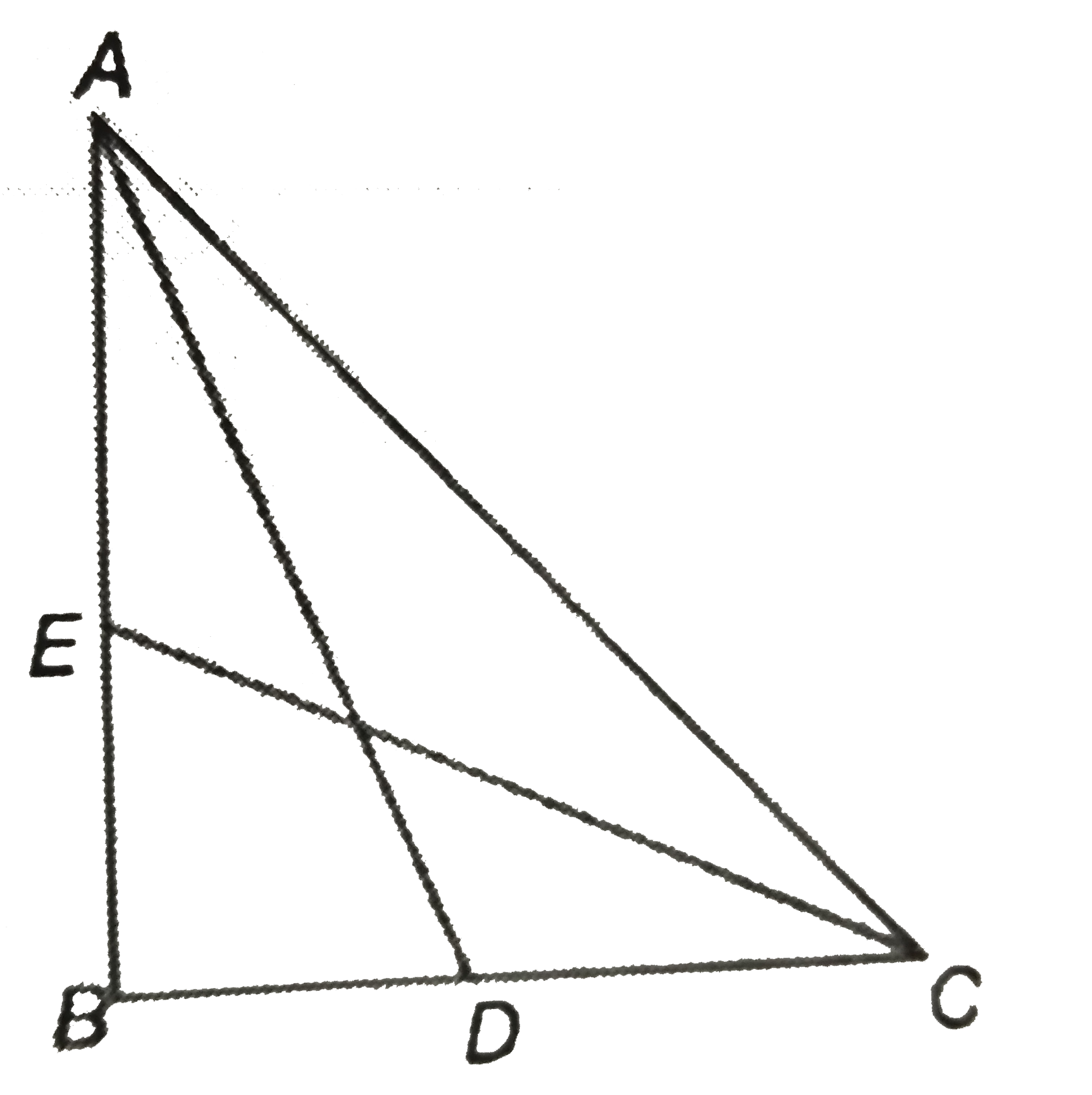
In the given figure, (not be scale), E and D are the mid-points of AB and BC respectively. Also, cm and cm. Find the .
15
18
20
24
The correct Answer is:C
i) Use Pythagora's theorem.
ii) Let AE=BE= and BD=CD=y.
iii) Use Pythagora's theorem in the right triangles ABD and BEC and obtain the equations in terms of and y.
iv) Add the above equations and obtain AC, i.e., .
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
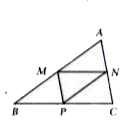
If the given figure , M, N and P are the mid-points of AB,AC and BC respectively. If MN=3 cm, NP=3.5 cm and MP=2.5 cm, calculate BC , AB and AC
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View Solution
Knowledge Check
Area of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
A10B7.5C15Dnone of theseArea of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
A10cm2B7.5cm2C15cm2Dnone of theseIn △ABC, M,N and P are the mid-points of AB,AC and BC respectively. If MN=3cm,NP=3.5cm and MP=2.5cm, calculate BC,AB and AC.
ABC = 6 cm
AB = 7cm
AC = 5cmBBC = 6 cm
AB = 7cm
AC = 8cmCBC = 6 cm
AC = 7cm
AB = 5cmDnone of these
In the given figure, a circle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the lengths AD, BE and CF.
View SolutionIf in ΔABC,∠B=90∘,AB=6√3 and AC=12cm, find BC.
View SolutionIn Δ ABC, DE || AC, D and E are two points on AB and CB respectively, If AB=10 cm and AD =4 cm, then BE : CE is
View SolutionIn a ΔABC,DandEare points on AC and BC respectively, AB and DE are perpendicular to BC. If AB=9cm,DE=3cmandAC=24cm, then AD is :
View SolutionIn Δ ABC, D, E, F are mid-points of AB, BC, CA respectively and ∠B=90∘, AB = 6 cm, BC = 8 cm. Then area of Δ DEF (in sq.cm) is
View Solution
