In △ABC, P is the mid-point of BC and Q is the mid-point of AP. Find the ratio of the area of △ABQ and the area of ∠ABC. The following are the steps involved in solving the above problem.
A) We know that a a median of a triangle divides a triangle into two triangles of equal area.
B) ⇒Ar(△ABP)=12[Ar(△ABC)]
C) Ar(△ABQ)=12[Ar(△ABP)]=14[Ar(△ABC)]
D) ⇒(△ABQ):Ar(△ABC)=1:4
ABCD
ADBC
ABCD
ADCB
The correct Answer is:B
ABCD is a required sequential order.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View SolutionABCD is a square. E is the mid-point of BC and F is the mid-point of CD . The ratio of the area of triangle AEF to the area of the square ABCD is (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 3 : 8
View Solution
Knowledge Check
If △ABC - △PQR and BCQR = 14 then ar(△PQR)ar(△ABC) =
A14B41C116D161If ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
A√k21+k22+k23B√k1k2k3k21+k22+k23C√∣∣(k21+k22−k23)∣∣D√∣∣(k21−k22−k23)∣∣
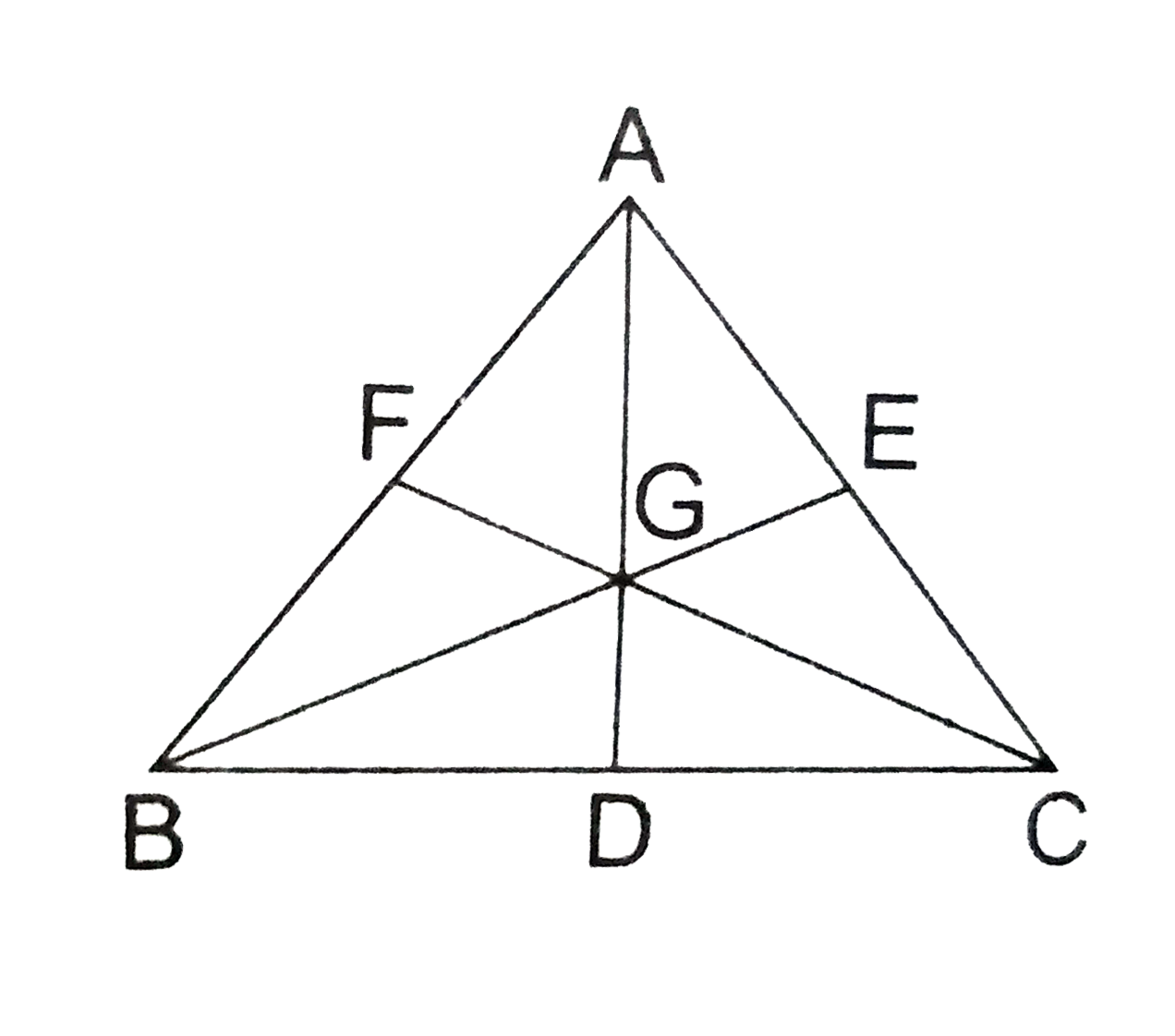
If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionIf the mid points of the sides of a triangle are (0,0),(1,2),(−3,4) then find area of triangle
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View Solution
