In a Roman steelyard, the weight of the rider is 25 dyne. When an unknown load is attached 5 cm from the point of suspension, the rider had to be moved by 35 cm. Calculate the unknown load
For Roman steelyard
L=R×OHHA
Where L = unknown load
OX = distance moved by rider.
HA = distance of the load from point of suspension
∴L=25dyne×35cm5cm=175 dyne
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Very Short Answer Type Questions30videos
SIMPLE MACHINES
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Short Answer Type Questions13videos
SIMPLE MACHINES
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODERN PHYSICSEXERCISE - Level 35videos
MODERN PHYSICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVES MOTION AND SOUND EXERCISE - Level 310videos
WAVES MOTION AND SOUND
Similar Questions
A balance similar to a Roman steel yard is constructed such that the length of the scale on the beam of the balance is 50 cm and the least count on the scale is 1 mm. The zero mark of the scale is at a distance of 15 cm from the point of suspension of the balance. The hook that is used to attach the loads and the centre of gravity of the beam are at distance 8 cm and 5 cm, respectively, from its fulcrum. If the weight of the rider of the balance is 50 gf, find the weight of the beam, the maximum load that can be measured using the balance and its least count.
View SolutionA uniform metre scale 1 m long is suspended at 50 cm division. A known weight of 160 gwt is tied at 80 cm division and the scale is balanced by a weight of 240 gwt tied to the scale at a certain distance from the point of suspension on the opposite side. Calculate this distance.
View Solution
Knowledge Check
- Question 1 - Select One
A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is
A3ΩB4ΩC5ΩD6Ω - Question 2 - Select One
Consider a metre bridge whose length of wire is 2m. A resistance of 10Ω is connected across one gap of the meter bridge and an unknown resistance is connected across the other gap. When these resistances are interchanged, the balance point shifts by 50 cm. What is the value of the unknown resistance?
A250ΩB10ΩC16.7ΩDNone of the above
A wire of length 2 m is fixed, as shown. When a load is suspended from the center, it sags by 2 cm. Find the strain.
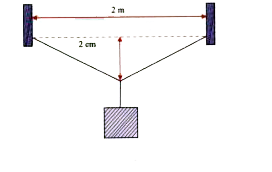 View Solution
View SolutionIn a meter bridge when the resistance in the left gap is 4Ω and an unknown resistance in the right gap the balance point is obtained at 40cm from the zero end. On shunting the unknown resistance with 4Ω, find the shift of the balance point on the bridge wire
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω, find the shift of the balance poiont on the bridge wire.
View SolutionDraw a circle with centre O and radius 3.5 cm. Take a point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
View SolutionAn unknown resistance 'X' is placed in the left gap and and a known resistance of 60Ω is plaecd in the right gap of metre bridge. The null point is obtained at 40 cm from the left end fo the bridge. Fid the unknown resistance.
View Solution

