Two slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is Solution in Kannada
K1θ1+K2θ2θ1+θ2
K1θ1d1+K2θ2d2K1d2+K2d1
K1θ1d+K2θ2d1K1d2+K2d1
K1θ1+K2θ2K1+K2
The correct Answer is:C
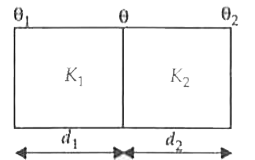 For the first slab
For the first slab
Heat current, H1=K1(θ1−θ)Ad1
For the second slab Heat current , H2=K2(θ−θ2)Ad2
As the slabs are connected in seriews same anount of heat current flows through the slabs
∴,.H1=H2
K1(θ1−θ)Ad1=K2(θ−θ2)Ad2
K1θ1d2−K1θd2=K2θd1−K2θ2d1
θ(K2d1+K1d2)=K1θ1d2+K2θ2d1
θK1θ1d2+K2θ2d1K2d1+K1d2
Topper's Solved these Questions
Similar Questions
In ruby laser, the stimulated emission is due to transition from
View SolutionWhich of the following graphs correctly represents the variation of heat energy (U) produced in a metallic conductor in a given time as a function of potential difference (V) across the conductor ?
View SolutionTwo conductors of same cross-section and conductivities K, 3K and length 3 d and d respectively are connected end to end as shown in figure. Temperature of end of first conductor is theta_(1) and that of second conductor is theta_(2) .the temperature of junction is steady state is (theta_(2)gttheta_(1))
View SolutionTwo plates each of area A thickness L1 and L2 thermal conductivities K1 and K2 respectively are joined to from a single plate of thickness (L1+L2) If the temperatures of the free surfaces are θ1 and θ2 Calculate
(a) Rate of flow of heat
(b) Temperature of interface
 .
.
View SolutionThree rods AB,BC and BD having thremal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in The ends A,C and D are at temperature theta_(1),theta_(2) and theta_(3) respectively Find the temperature of the junction B (Assume steady state and theta_(1)gt theta gt theta_(2)gttheta_(3)) .
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K_(1) and K_(2) . The temperature of the free ends of the first and seconds rods are maintained at theta_(1) and theta_(2) respectively. The temperature of the common junction is
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionTwo slabs A and B of different materials but of the same thickness are joined end to end to form a composite slab. The thermal conductivities of A and B are K1 and K2 respectively. A steady temperature difference of 12∘C is maintained across the composite slab. If K1=K22, the temperature difference across slab A is
View SolutionTwo T.G's having reduction factor K1 and K2 are connected series and give deflections θ1andθ2 respectively . Then K1:K2
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are theta_(2) and theta_(1) respectively, (theta_(2) gt theta_(1)) The temperature at the interface is:
View SolutionTwo slabs A and B of different materials but of the same thickness are joined end to end to form a composite slab . The thermal conductivities of A and B are K1 and K2 respectively . A steady temperature difference of 12∘C is maintained across the composite slab . If K1=K22 , the temperature difference across slab A is
View SolutionTwo different metal rods of the same length have their ends kept at the same temperature theta_(1) , and theta_(2) with theta_(2) gt theta_(1) . If A_(1) and A_(2) are their cross-sectional areas and K_(1) and K_(2) their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
View Solutionदिखाए गए चित्रानुसार 3K तथा K उष्माचालकता गुणांक एवं क्रमशः d तथा 3d मोटाई वाले दो पदार्थो जो जोड़कर एक पट्टिका बनायी गयी है। उनके बाहरी सतहों के तापमान क्रमशः θ2 और θ1 है (θ2>θ1) अंतरपृष्ठ का तापमान है
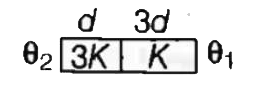
View SolutionDefine coefficient of thermal conductivity. Two metal slabs of same area of cross-section, thickness d_(1) and d_(2) having thermal conductivities K_(1) and K_(2) respectively are kept in contact. Deduce expression for equivalent thermal conductivity.
View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
View Solution
