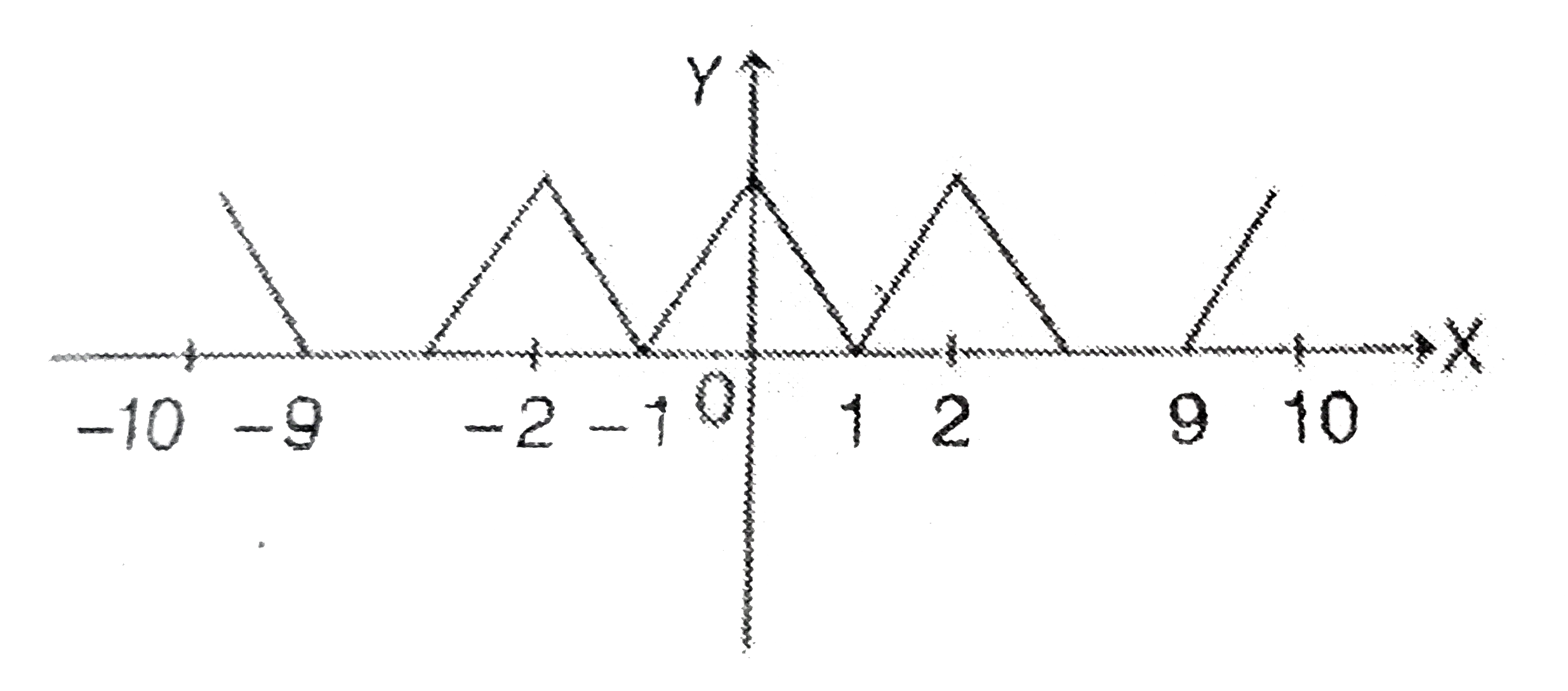
For any real number x,let[x]
denote the largest integer less than or equal to x, Let f
be a real-valued function defined on the interval [−10,10]
be
f(x)={x−[x]if[x] is odd1+[x]−xif[x] is even.
Then the value of π210∫10−1f(x)cosπxdx is____
The correct Answer is:4
Given , f (x) ={x−[x],if[x] is odd1+[x]−x,if[x] is even. f (x) and cosπx both are periodic with period 2 and both are even .
∴∫10−10f(x)cosπxdx=2∫100f(x)cosπxdx
=10∫20f(x)cosπxdx
Now , ∫10f(x)cosπxdx
=∫10(1−x)cosπxdx=−∫10ucosπxdu
and
∫21f(x)cosπxdx=∫21(x−1)cosπxdx
=−∫10ucosπudu
∴∫10−10f(x)cosπxdx=−20∫10ucosπudu=40π2
⇒π210∫10−10f(x)cosπxdx=4
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - ESTIMATION, GAMMA FUNCTION AND DERIVATIVE OF INDEFINITE INTEGRAL22videos
DEFINITE INTEGRATION
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - LIMITS AS THE SUM6videos
DEFINITE INTEGRATION
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - LIMITS AS THE SUM6videos
DEFINITE INTEGRATION
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)1videos
COMPLEX NUMBERS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - TOPIC 3 APPLICATIONS OF HOMOGENEOUS DIFFERENTIAL EQUATIONS <br> ANALYTICAL & DESCRIPTIVE QUESTIONS7videos
DIFFERENTIAL EQUATIONS
Similar Questions
f(x)={x−[x],if[x]is odd1+[x]−x,if[x] is even
Then, the value of π210∫10−10f(x)cosπ×dx isView SolutionFor any real number x,let[x] denote the largest integer less than or equal to x,Letf be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x]isodd1+[x]−x,if[x]iseven Then the value of π210∫10−1f(x)cosπxdxis__
View Solution
Knowledge Check
- Question 1 - Select One
For any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
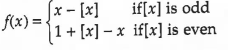 Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1
Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1 - Question 2 - Select One
For any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx isA2B4C0DNone of these - Question 3 - Select One
For a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
AIf is differentiable on R.Bf is symmetric about the line x=0C∫3−3f(x)dx=0DFor each real α, the equation f(x)−α=0 has infinitely many roots.
For any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
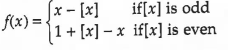 Then, the value of (π10)2(∫10−10f(x)cosπxdx isView Solution
Then, the value of (π10)2(∫10−10f(x)cosπxdx isView SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let f: R→ R be defined as f(x)=2x+[x]+sinxcosx then f is
View SolutionFor any real number x, let [x] denote the largest integer less than or equal to x. If
∫100[√10xx+1]dx then the value of 9I isView SolutionFor a real number x, lel [x] denotes the griater + integer less than or equal to x. let f:R→R be defined by f(x)=2x+[x] then f is:
View SolutionLet [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View Solution

