A truck has to carry a load in the shortest time from one point to another at a distance L from the first.It can only start up or slow down at the same acceleration a. What maximum velocity must the truck attain to satisfy this condition ?
√La
√2La
√3La
√5La
The correct Answer is:A
Let v be the maximum velocity attained and t the total time of journey. t. is the duration of acceleration and retardation. Then v=0+at.
∴L=12at.2+v(t−2t.)+12at.2
=a(va)2+v(t−2va)=v2a+vt−2v2a=vt−v2a
t=Lv+va⇒dtdv=−Lv2+1a When t is minimum, dtdv=0∴vmax=√La
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-1
70 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
- MOVING CHARGES AND MAGNETISM BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 2 : Concept Applicator
25 Videos
Similar Questions
A stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point p. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
View SolutionFrom point A located on a highway (figure) one has to get by car as soon as possible to point B located in the field at a distance l from the highway. It is known that the car moves in the field η times slower than on the highway. At what distance from point D one must turn off the highway?

View Solution
Knowledge Check
A train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
Find the critical distance Sc for which passenger will take the ten seconds time to catch the trainA50 mB35 mC30 mD25 mA wire of length L, mass m and carrying a current I is suspended from point O as shown, An another infinitely long wire carrying the same current I is at a distance L below the lower end of the wire. Given i=2A, L=1m and m=0.1kg (In 2=0.693)
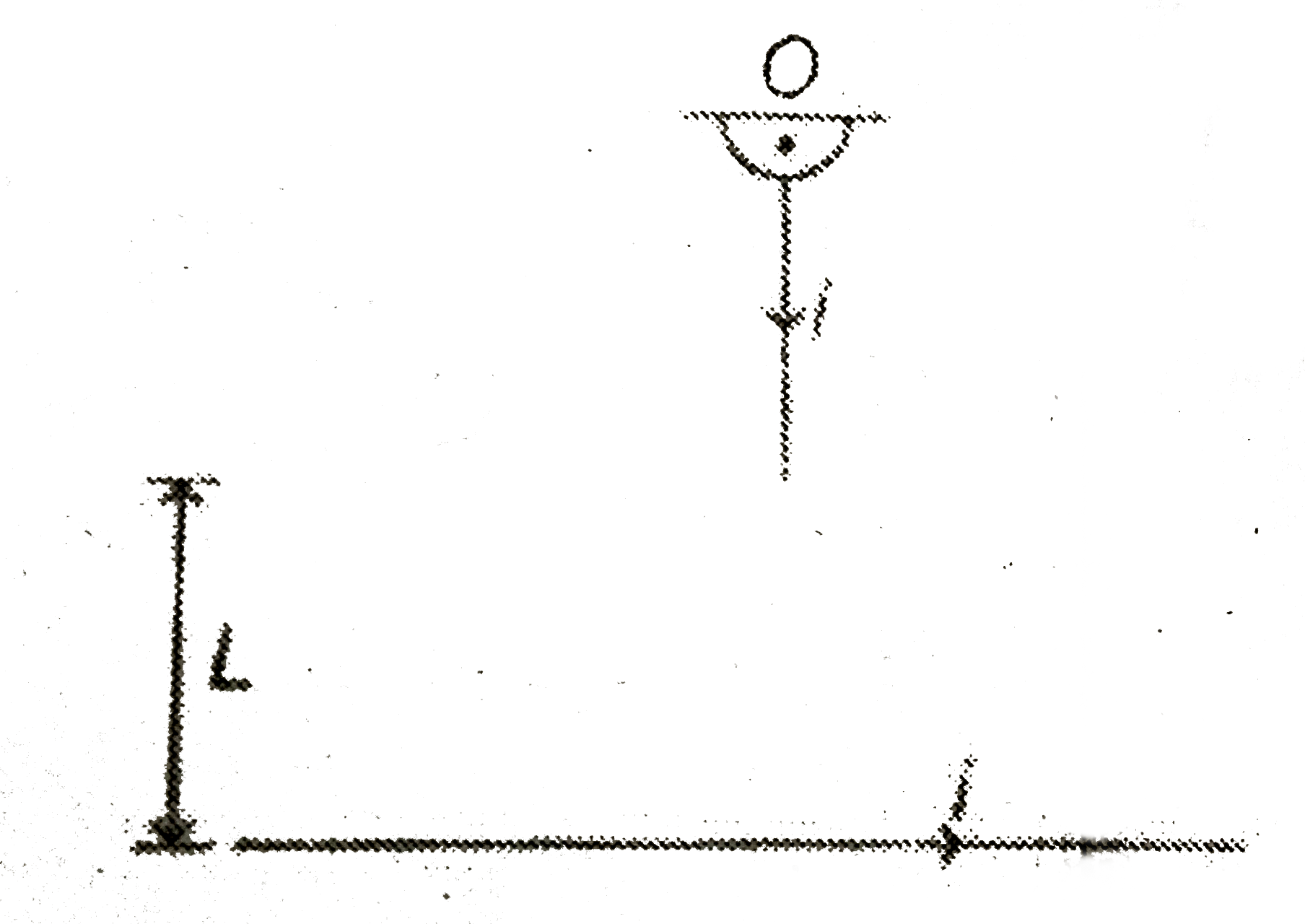
What is the angular acceleration of the wire just after it is released from the position shown ?A6.2×10−8rds2B2.1×10−4rds2C4.5×10−5rds2D9.3×10−6rds2Two buses start from the opposite points of a main road, 150 km apart. The first bus runs for 25 km and takes a right turn and then runs for 15 km. It then turns left and runs for another 25 km and takes the direction back to reach the main road. In the meantime, due to a minor break down, the other bus has run only 35 km along the main road. What would be the distance between the two buses at this point ?
A65 kmB75 kmC80 kmD85 km
An object starts from rest from the point A to rest at point B on the same straight line at a distance d. It moves over the first part of the distance with an acceleration αm/s2 and for the remainder the retardation βm/s2. Find the time taken to complete the journey.
View SolutionA point move in a straight line so that its distance from the start in t sec is equal to s=14t4−4t3+16t2. What will be acceleration and at what times is its velocity equal to zero?
View SolutionA body begins to move with an initial velocity of 2ms−1 and continues to move at a constant acceleration a.Ten seconds later a second body begins to move from the same point with an initial velocity of 12ms−1 in the same direction with the same acceleration.What is the maximum acceleration at which it would be possible for the second body to overtake the first ?
View SolutionAn automobile and a truck start from rest at the same instant, with the automobile initially at some distance behind the truck. The truck has a constant acceleration of 2.2m/s2 and the automobile has an acceleration of 3.5m/s2. The automobile overtakes the truck when it (truck) has moved 60 m.
(a) How much time does it take the automobile to overtake the truck ?
(b) How far was the automobile behind the truck initially ?
(c) What is the speed of each during overtaking ?
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View Solution
