Starting from rest a particle moves in a straight line with acceleration
a=(25−t2)1/2m/s2 for 0≤t≤5s
a=3π8m/s2 for t>5s
The velocity of particle at t=7s is:
11m/s
22m/s
33m/s
44m/s
The correct Answer is:B
V7=V5+3π8×2 To calculate V5 i.e., velocity at end of 5 sec.
a=(25−t2)1/2⇒dvdt=(25−t2)1/2
∫dv=∫5(25−25sin2θ)1/2cosθdθ⎧⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪⎩t=5sinθdtdθ=5cosθt0,θ=0t=5,θ=π2
=π/2∫05×4cos2θdθ=25π4
V7=25π4+3π4=28π4=7π=22m/s
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-170videos
MOTION IN A STRAIGHT LINE
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR28videos
MOTION IN A PLANE
- BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 2 : Concept Applicator25videos
MOVING CHARGES AND MAGNETISM
Similar Questions
A particle starts from rest at t=0 and moves along a straight line with a variable acceleration given by a (t)=(3t+1)ms−2 ,where t],[ is in seconds.The velocity of the particle at t=4s is
View SolutionA particle moves in a straight line with an acceleration a m/s^(2) at time t seconds,where a=-(1)/(t^(2)) .When t=1 the particle has a velocity of 3m/s .If the velocity of the particle at t=4s is (9)/(n)ms^(-1) The value of n is
View Solution
Knowledge Check
- Question 1 - Select One
Starting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
AAt t=2s, the position of the particle is at x=9mBParticle acceleration at t=2s is 1m/s2CParticle acceleration is 1/2m/s2 through out the motionDParticle will never go in negative direction from it's starting position - Question 2 - Select One
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 A2m/sB3m/sC4m/sD6m/s
A2m/sB3m/sC4m/sD6m/s - Question 3 - Select One
A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
A15 mB30 mC45 mD60 m
[" A particle starts from "],[" rest at "t=0" and moves "],[" along a straight line with "],[" a variable acceleration "],[" given by a "(t)=(3t+1)ms^(-2)],[" where "t" is in seconds."],[" The velocity of the "],[" particle at "t=4s" is "]
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
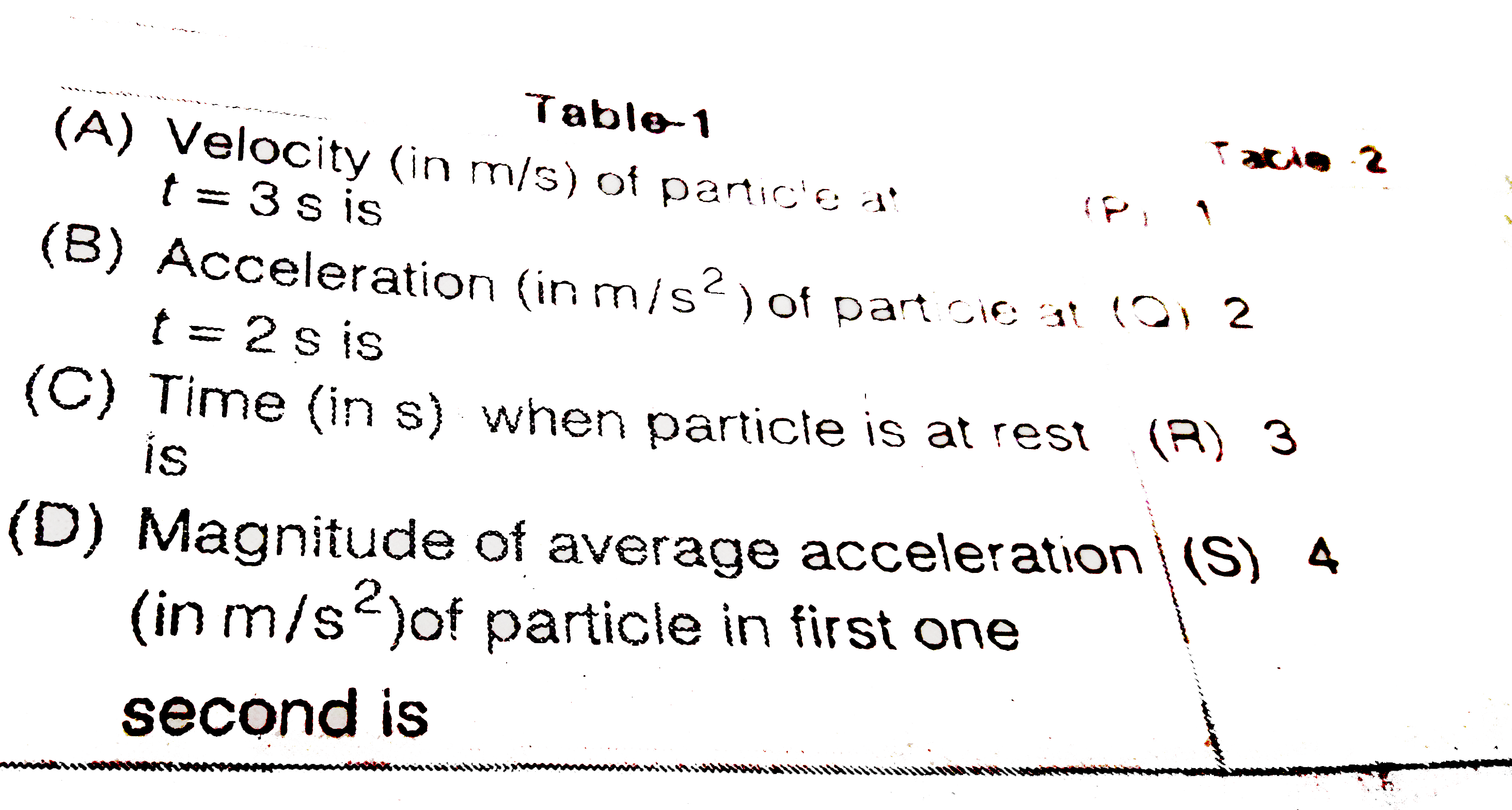 View Solution
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View SolutionA particle is moving in a straight line under constant acceleration of 4m/s2. If its velocity at t=0 is 10 m//s, the displacement of particle in the 5th second of its motion is
View Solution

