Figure shows a bob of mass m suspended from a string of length L.The velocity is v0 at A,then the porential energy of the system is ______ at the lowes point A.

12mv20
mgh
−12mv20
zero
The correct Answer is:D
At the lowest point ,h-0 ∴ P.E.=O (gravitational P.E.) There is no work done on the bob by the tension as it is perpendicular to the displacement.
∴ Potential energy is associated only to the gravitaional force.
Topper's Solved these Questions
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 3:Power)
20 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 4:Collisions)
1 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topicwise)
34 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-2 Concept Applicator
23 Videos
Similar Questions
A bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
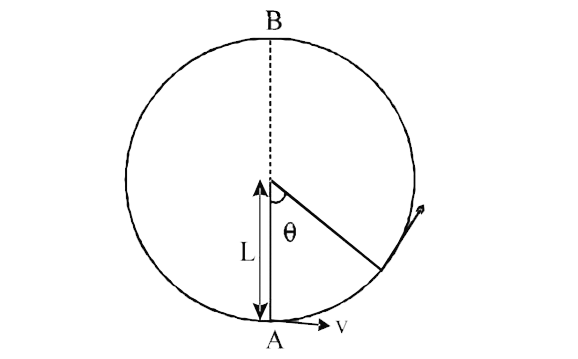
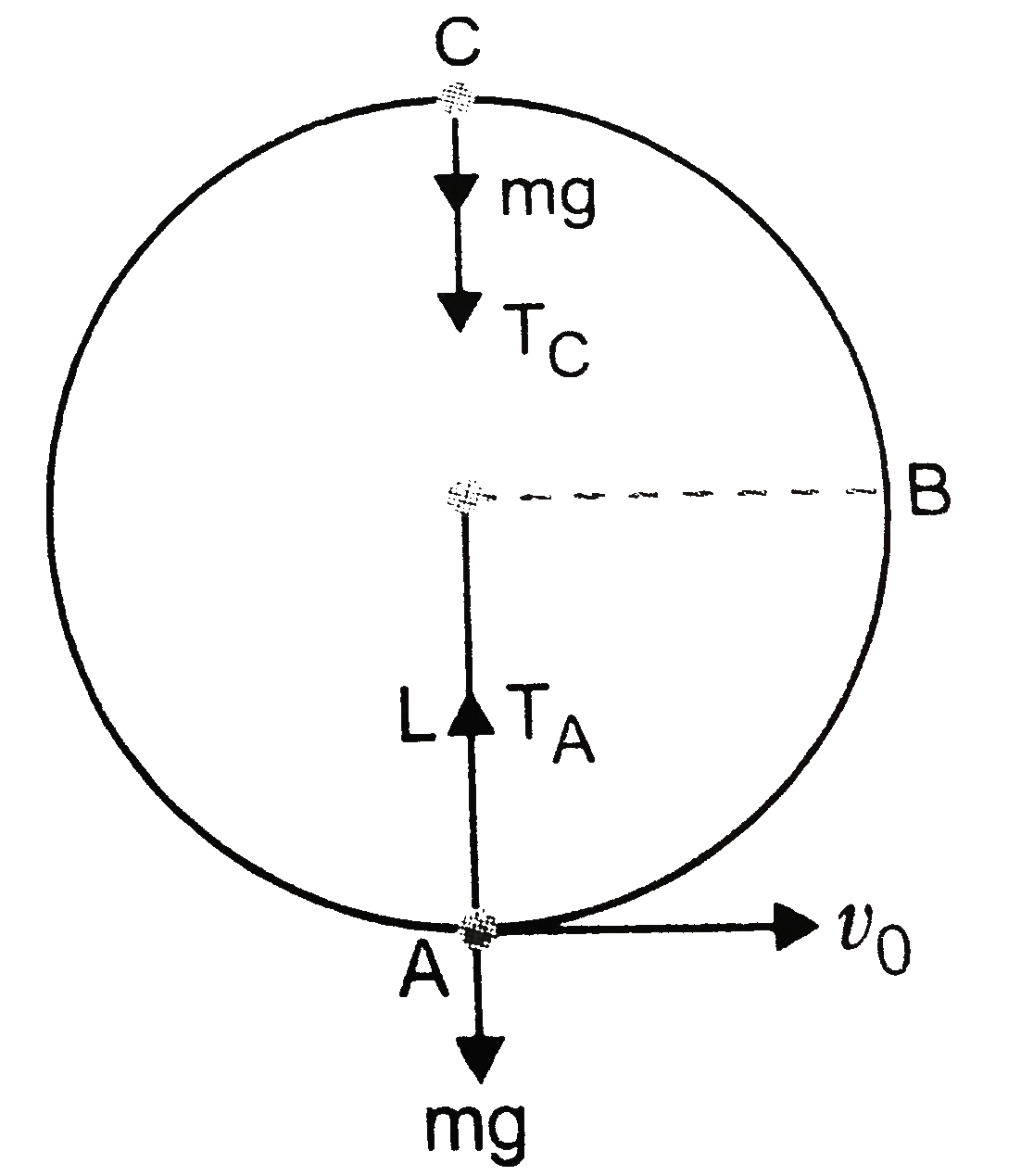
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
View Solution
Knowledge Check
A mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
A√3glB√4glC√5glD√6glA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-q
AA-p,B-q,C-s,D-rBA-q,B-r,C-q,D-sCA-r,B-s,C-q,D-pDA-s,B-p,C-r,D-qA particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
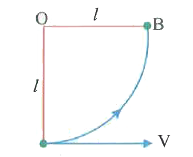 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2gl
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View SolutionA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View SolutionThe minimum velocity required to complete a full circle in a vertical plane is given to a bob of mass m suspended by a string of length 25 cm. When it reaches the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. After the collision, if the second bob acquires the minimum speed required to complete a full circle in the vertical plane, then the length of the string l2 __m. (Both the strings are massless and in-extensible)
View SolutionA bob of mas M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies.
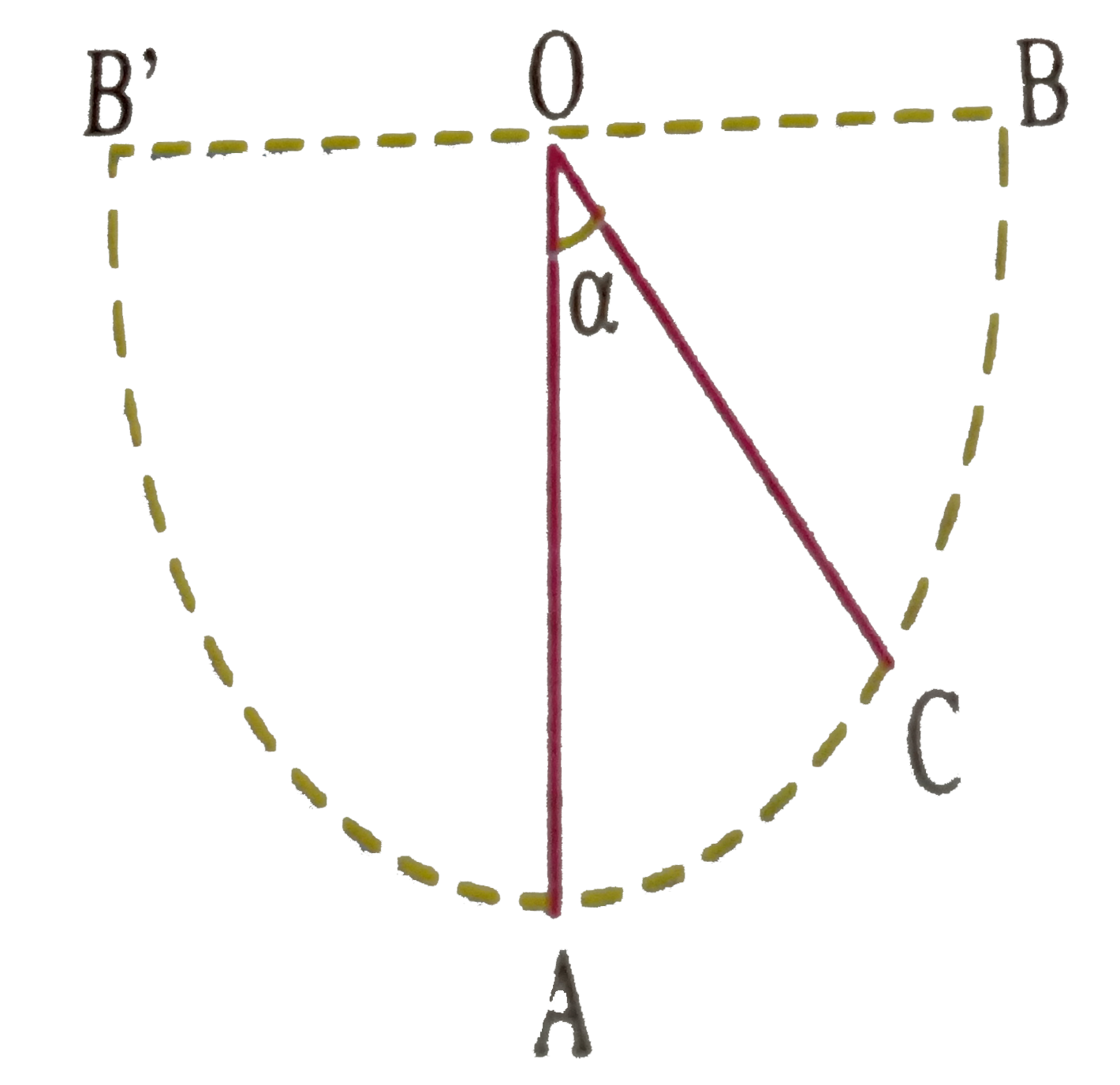 .
.
View SolutionA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View Solution
