A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
1
3
5
1/5
The correct Answer is:C
To solve the problem, we need to analyze the motion of the two bobs and the conditions for them to complete a full vertical circle.
1. Understanding the Minimum Velocity for Circular Motion:
- For a bob to complete a full vertical circle, the minimum velocity at the topmost point is given by:
vmin=√gL
- At the bottom of the circle, the minimum velocity required is:
vmin=√5gL
- Here, L is the length of the string.
2. Initial Conditions for the First Bob:
- The first bob (mass m, length l1) is given a minimum velocity to complete the circle. At the bottom, its velocity is:
v1=√5gl1
- At the top of the circle, its velocity will be:
vtop=√gl1
3. Collision with the Second Bob:
- The second bob (mass m, length l2) is initially at rest. When the first bob collides elastically with the second bob at the top of its path, the velocities will exchange due to the elastic collision of two equal masses.
- After the collision, the first bob will have a velocity of 0 (as it transfers its momentum), and the second bob will have a velocity of:
v2=√gl1
4. Minimum Velocity for the Second Bob:
- For the second bob to complete a full vertical circle, after the collision, it must have a minimum velocity at the top given by:
vmin=√gl2
- Setting the velocity of the second bob after the collision equal to the minimum required for it to complete the circle gives us:
√gl1=√5gl2
5. Solving for the Ratio:
- Squaring both sides to eliminate the square roots:
gl1=5gl2
- Dividing both sides by g (which is non-zero):
l1=5l2
- Thus, the ratio of the lengths of the strings is:
l1l2=5
Final Answer:
The ratio l1l2 is 5.
---
- For a bob to complete a full vertical circle, the minimum velocity at the topmost point is given by:
vmin=√gL
- At the bottom of the circle, the minimum velocity required is:
vmin=√5gL
- Here, L is the length of the string.
- The first bob (mass m, length l1) is given a minimum velocity to complete the circle. At the bottom, its velocity is:
v1=√5gl1
- At the top of the circle, its velocity will be:
vtop=√gl1
- The second bob (mass m, length l2) is initially at rest. When the first bob collides elastically with the second bob at the top of its path, the velocities will exchange due to the elastic collision of two equal masses.
- After the collision, the first bob will have a velocity of 0 (as it transfers its momentum), and the second bob will have a velocity of:
v2=√gl1
- For the second bob to complete a full vertical circle, after the collision, it must have a minimum velocity at the top given by:
vmin=√gl2
- Setting the velocity of the second bob after the collision equal to the minimum required for it to complete the circle gives us:
√gl1=√5gl2
- Squaring both sides to eliminate the square roots:
gl1=5gl2
- Dividing both sides by g (which is non-zero):
l1=5l2
- Thus, the ratio of the lengths of the strings is:
l1l2=5
The ratio l1l2 is 5.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT18videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON15videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
Similar Questions
A mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The angle θ isView SolutionA ball of mass m moving with a speed u0 collides elastically with a rod of mass M suspended in the vertical plane by the hinge O. The rod is free to rotate in the vertical plane. Before and after the collision.
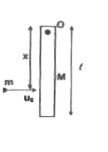 View Solution
View SolutionA bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
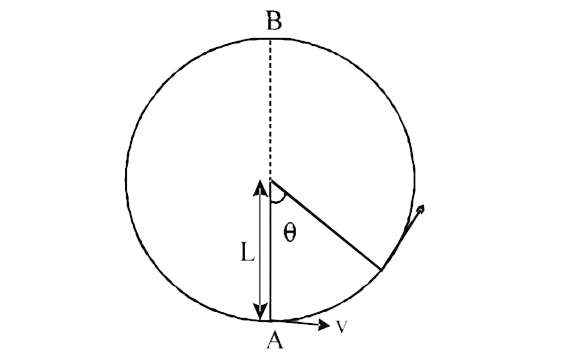 View Solution
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
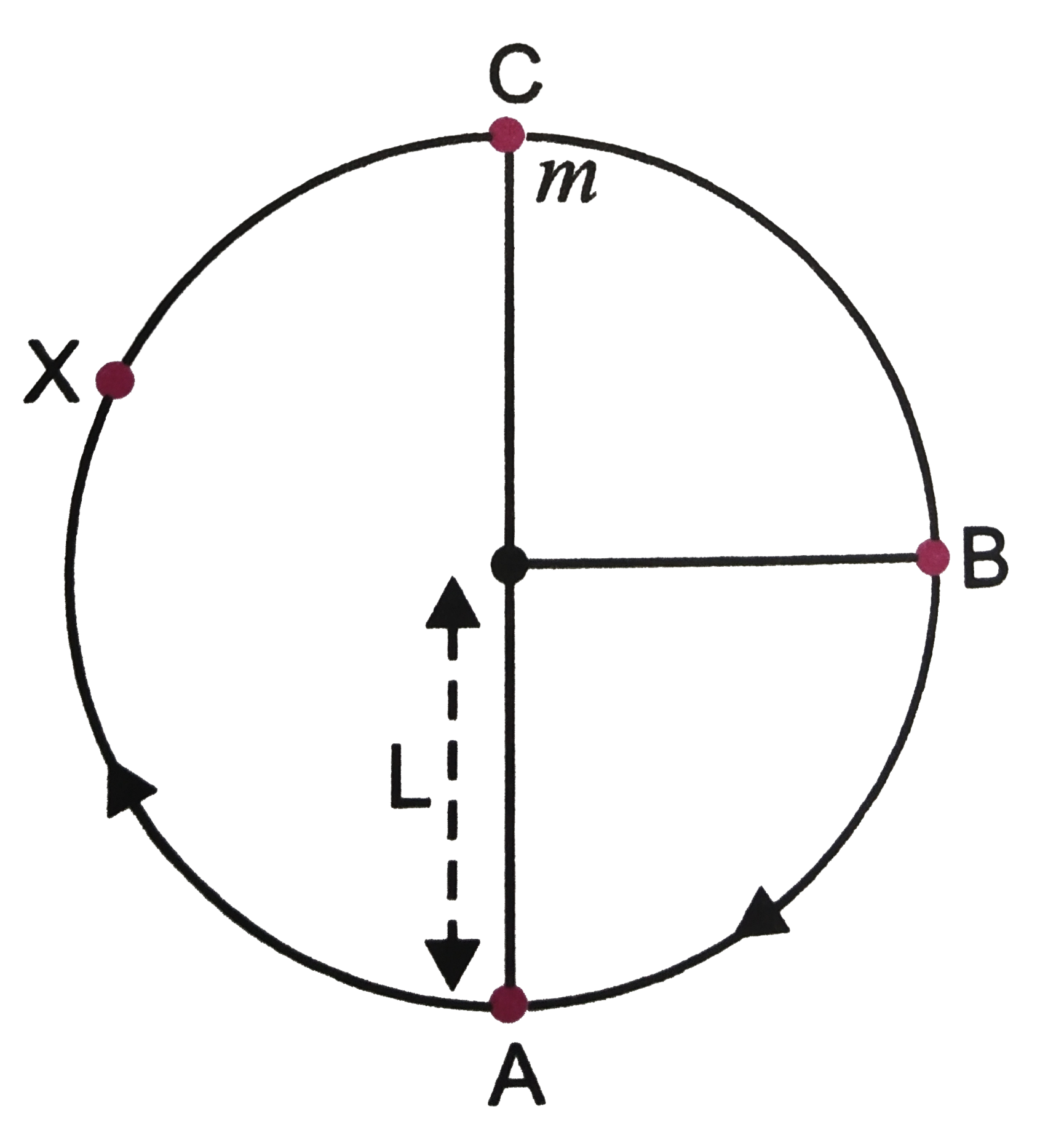 View Solution
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet isView SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant isView SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View Solution

