A spring of unstretched length l has a mass m with one end fixed to a rigid support.Assuming spring to be made of a uniform wire,the kinetic energy possessed by it is its free end is pulled with uniform velocity v is :
12mv2
mv2
13mv2
16mv2
The correct Answer is:D
To solve the problem, we need to find the kinetic energy possessed by a spring when its free end is pulled with a uniform velocity v.
1. Understanding the Spring's Properties:
- The spring has an unstretched length l and a mass m.
- The spring is assumed to be made of a uniform wire, which means its mass is distributed evenly along its length.
2. Calculating Linear Mass Density:
- The linear mass density λ of the spring can be calculated as:
λ=ml
- This gives us the mass per unit length of the spring.
3. Considering an Element of the Spring:
- Let’s consider a small element dx of the spring at a distance x from the fixed end.
- The mass of this small element dm can be expressed as:
dm=λdx=mldx
4. Finding the Velocity of the Element:
- When the free end of the spring is pulled with a velocity v, the velocity of the element at distance x from the fixed end can be determined by the proportionality of the distance:
vx=xlv
- This means that the velocity of each element varies linearly from 0 (at the fixed end) to v (at the free end).
5. Calculating Kinetic Energy of the Element:
- The kinetic energy dK of the small element dm is given by:
dK=12dmv2x
- Substituting dm and vx:
dK=12(mldx)(xlv)2
dK=12mlx2v2l2dx
dK=mv22l3x2dx
6. Integrating to Find Total Kinetic Energy:
- To find the total kinetic energy K of the entire spring, we integrate dK from 0 to l:
K=∫l0mv22l3x2dx
- Evaluating the integral:
K=mv22l3(x33)l0=mv22l3⋅l33=mv26
Final Result:
The total kinetic energy possessed by the spring when its free end is pulled with a uniform velocity v is:
K=mv26
- The spring has an unstretched length l and a mass m.
- The spring is assumed to be made of a uniform wire, which means its mass is distributed evenly along its length.
- The linear mass density λ of the spring can be calculated as:
λ=ml
- This gives us the mass per unit length of the spring.
- Let’s consider a small element dx of the spring at a distance x from the fixed end.
- The mass of this small element dm can be expressed as:
dm=λdx=mldx
- When the free end of the spring is pulled with a velocity v, the velocity of the element at distance x from the fixed end can be determined by the proportionality of the distance:
vx=xlv
- This means that the velocity of each element varies linearly from 0 (at the fixed end) to v (at the free end).
- The kinetic energy dK of the small element dm is given by:
dK=12dmv2x
- Substituting dm and vx:
dK=12(mldx)(xlv)2
dK=12mlx2v2l2dx
dK=mv22l3x2dx
- To find the total kinetic energy K of the entire spring, we integrate dK from 0 to l:
K=∫l0mv22l3x2dx
- Evaluating the integral:
K=mv22l3(x33)l0=mv22l3⋅l33=mv26
The total kinetic energy possessed by the spring when its free end is pulled with a uniform velocity v is:
K=mv26
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 3:Power)20videos
CONCEPT BUILDER
- BOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 4:Collisions)1videos
CONCEPT BUILDER
- BOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topicwise)34videos
CONCEPT BUILDER
- BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator30videos
COMMUNICATION SYSTEM
- BOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-2 Concept Applicator23videos
CURRENT ELECTRICITY
Similar Questions
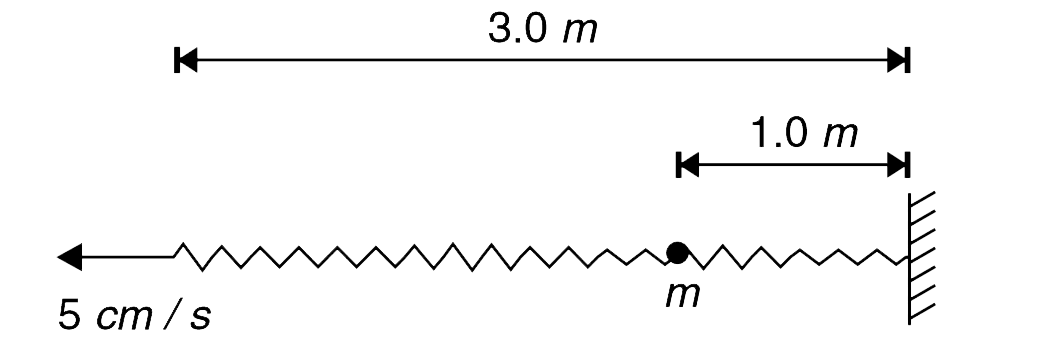
A uniform light spring has unstretched length of 3.0 m. One of its end is fixed to a wall. A particle of mass m = 20 g is glued to the spring at a point 1.0 m away from its fixed end. The free end of the spring is pulled away from the wall at a constant speed of 5 cm/s. Assume that the spring remains horizontal (i.e., neglect gravity). Force constant of spring = 0.6 N / cm.
(a) With what speed does the particle of mass m move?
(b) Find the force applied by the external agent pulling the spring at time 2.0 s after he started pulling.
 View Solution
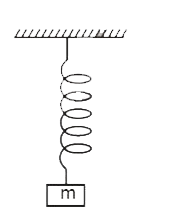
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
AMgBMg(L−y)/LCMgL/(L−y)DMgy/L - Question 2 - Select One
One end of an ideal spring of unstreched length lO=1m, is fixed on a frictionless horizontal table. The other end has a small disc of mass 0.1kg attached to it. The disc is projected with a velocity υ0=11m/s perpendicular to the spring.

What is the force constant of spring?A210N/mB100N/mC110N/mD200N/m - Question 3 - Select One
One end of an ideal spring of unstreched length lO=1m, is fixed on a frictionless horizontal table. The other end has a small disc of mass 0.1kg attached to it. The disc is projected with a velocity υ0=11m/s perpendicular to the spring.
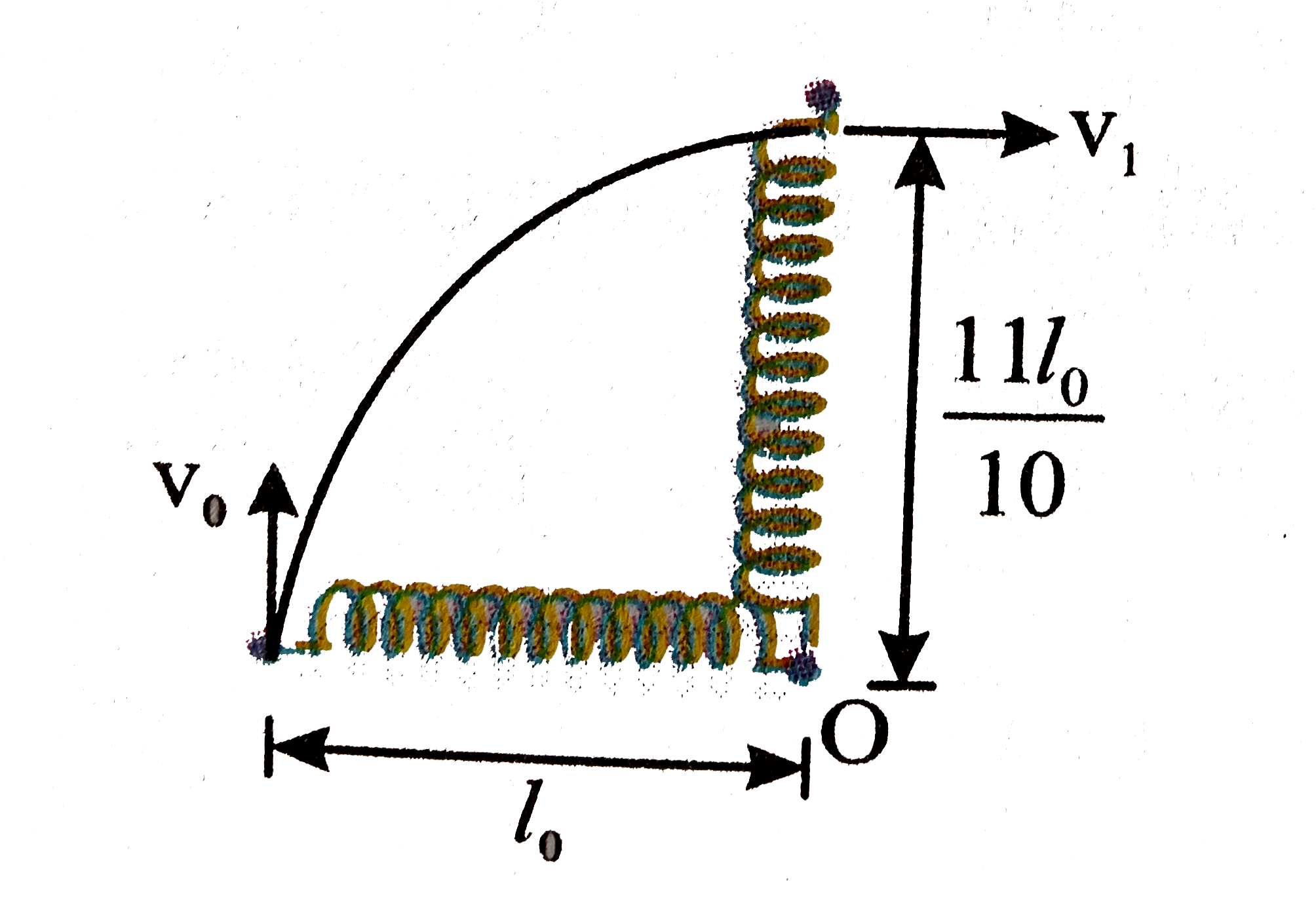
Choose the correct statementsAlinear momentum of disc is conserved as the spring force is always perpendicular to velocity of disc.Bangular momentum of disc about fixed end of spring is conservedCkinetic energy of disc is conservedDangular velocity of disc remains constant
A massless spring of natural length of 0.5 m and spring constant 50 N/m has one end fixed and the other end attached to a mass of 250 g. The spring mass system is on a smooth floor. The mass is pulled until the length of the spring is 0.6 m and then released from rest. The kinetic energy of the mass when the length of the spring is 0.5 m is
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
 View Solution
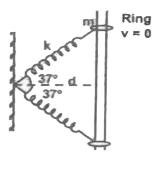
View SolutionOne end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
 View Solution
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 View Solution
View Solution

