A man stands in the middle of a rotating table which has an angular velocity ω He is holding two equal masses at arms lengtii ineach hand. Without moving his arms he just drops the two masses. How will be the angular speed of table get changed?
increase
decrease
become zero
remain constant
The correct Answer is:A
As mass decreases, moment of inertia I decreases. Since L=Iω is constant, therefore ω increases.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR28videos
SYSTEM OF PARTICLES & ROTATIONAL MOTION
- BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR28videos
SYSTEM OF PARTICLES & ROTATIONAL MOTION
- BOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR25videos
SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)28videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A student stands on a table rotating with an angular speed ω while holding two equal dumbbells at arm's length. With out moving anything else,the two dumbbells are dropped. What changes will be there in motion, if any? What would be the changes if he bring the dumbbells to keep in touch with his chest by folding his arms ? Explain
View SolutionTwo equal masses m are attached by a string. One mass lies at radial distance r from the centre of a horizontal turntable which rotates with constant angular velocity ω=2 rad s(1), while the second hangs from the string inside the tumtable's hollow spindle (see fig.) The coefficient of static friction between the turntable and the mass lying on it is μs=0.5. The maximum and minimum values of radius such that the mass lying on the turntable does not slide are rmax+rmin in meter is
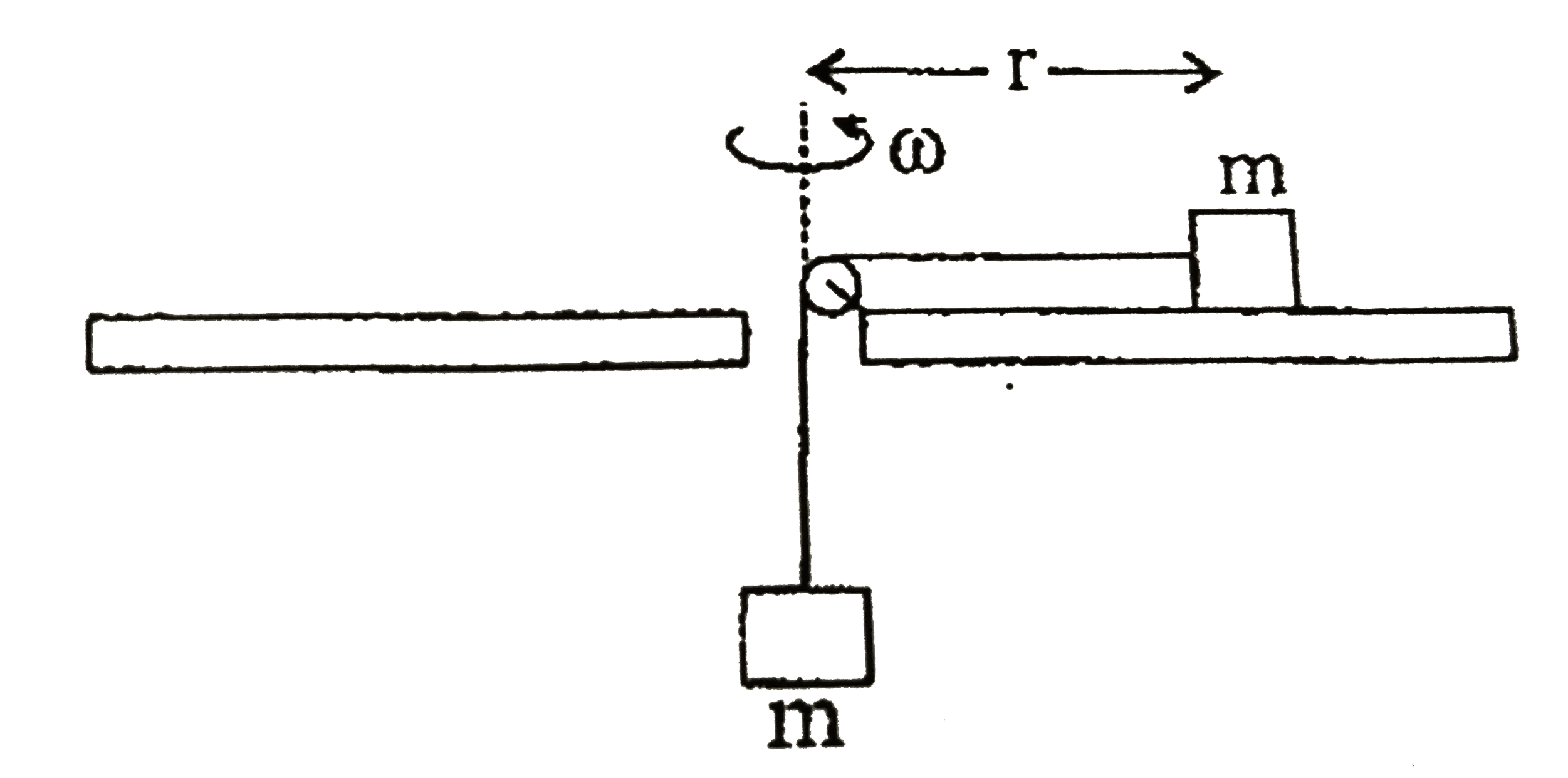 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A man turns on a rotating table with an angular velocity ω. He is holding two equal masses at arm's. Without moving his arms, he just drops the masses. Then his angular velocity
Aless than ωBmore than ωCequal to ωDany of these three - Question 2 - Select One
A person is sitting on a rotating chair which is rotating with some angular velocity. Person is sitting on the chair with his arms folded. Now he slowly stretches his arm then
AAngular momentum of the system decreases (BAngular momentum of the system increasesCAngular momentum remains constantDAngular speed of the system increases - Question 3 - Select One
A man stands at the centre of turn table and the turn table is rotating with certain angular velocity. If he walks towards rim of the turn table, then
Amoment of inertia of the system decreasesBangular momentum of system increasesCangular velocity of the system increasesDkinetic energy of the system decreases
A preson is standing on the centre of a rotating table with his arms outstretched. The table is rotating freely with an angular his hands towards his chest. The moment of inertia reduces to 35 time the original moment of inertia. Calculate angular speed of the man when he withdraws his hands.
View SolutionA rotating table has angular velocity 'ω' and moment of inertia I1. A person of mass 'm' stands on the centre of rotating table. If the preson moves a distance r along its radius then what will be thefinal angualr velcotiy of the rotating table ?
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beada are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpenducular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 View Solution
View SolutionA thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5kg is tied and a block of mass 8.0kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0kg to 1.0kg, what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
 View Solution
View SolutionA man is sitting on a rotating stool with his arms outstretched. If suddenly he folds his arms the angular velocity of the man would
View Solution

