Two capacitrors of 2μFand4μF are connected in parallel. A third capacitor of 6μF is connected in series. The combaination is connected across a 12 V battery. The voltage across 2μF capacitor is
2 V
8 V
6 V
1 V
The correct Answer is:C
To solve the problem of finding the voltage across the 2 µF capacitor when two capacitors (2 µF and 4 µF) are connected in parallel and then in series with a 6 µF capacitor across a 12 V battery, we can follow these steps:
1. Identify the Configuration:
- We have two capacitors, C1=2μF and C2=4μF, connected in parallel.
- A third capacitor, C3=6μF, is connected in series with the parallel combination of C1 and C2.
2. Calculate the Equivalent Capacitance of the Parallel Combination:
- The equivalent capacitance Ceq for capacitors in parallel is given by:
Ceq=C1+C2=2μF+4μF=6μF
3. Combine the Equivalent Capacitance with the Series Capacitor:
- Now, we have Ceq=6μF in series with C3=6μF.
- The formula for the equivalent capacitance Ctotal of capacitors in series is:
1Ctotal=1Ceq+1C3
- Substituting the values:
1Ctotal=16μF+16μF=26μF=13μF
- Therefore, the total capacitance is:
Ctotal=3μF
4. Calculate the Total Charge in the Circuit:
- The total charge Q stored in the capacitors when connected to a voltage V=12V is given by:
Q=Ctotal×V=3μF×12V=36μC
5. Determine the Voltage Across the Series Capacitors:
- The voltage across the series combination of the two capacitors Ceq and C3 is equal to the total voltage:
Vtotal=VCeq+VC3
- Since Ceq and C3 have the same capacitance, the voltage will split equally:
VCeq=VC3=Vtotal2=12V2=6V
6. Voltage Across the Parallel Capacitors:
- The voltage across the parallel capacitors C1 and C2 (which is VCeq) is the same as the voltage across each capacitor in that parallel combination:
VC1=VC2=VCeq=6V
Final Answer:
The voltage across the 2 µF capacitor is 6 V.
- We have two capacitors, C1=2μF and C2=4μF, connected in parallel.
- A third capacitor, C3=6μF, is connected in series with the parallel combination of C1 and C2.
- The equivalent capacitance Ceq for capacitors in parallel is given by:
Ceq=C1+C2=2μF+4μF=6μF
- Now, we have Ceq=6μF in series with C3=6μF.
- The formula for the equivalent capacitance Ctotal of capacitors in series is:
1Ctotal=1Ceq+1C3
- Substituting the values:
1Ctotal=16μF+16μF=26μF=13μF
- Therefore, the total capacitance is:
Ctotal=3μF
- The total charge Q stored in the capacitors when connected to a voltage V=12V is given by:
Q=Ctotal×V=3μF×12V=36μC
- The voltage across the series combination of the two capacitors Ceq and C3 is equal to the total voltage:
Vtotal=VCeq+VC3
- Since Ceq and C3 have the same capacitance, the voltage will split equally:
VCeq=VC3=Vtotal2=12V2=6V
- The voltage across the parallel capacitors C1 and C2 (which is VCeq) is the same as the voltage across each capacitor in that parallel combination:
VC1=VC2=VCeq=6V
The voltage across the 2 µF capacitor is 6 V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
Two capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is

View SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
View SolutionA capacitor of 20μF charged upto 500 V is connected in parallel with another capacitor of 10μF, which is charged upto 200 V. the common potential is
View SolutionThe potential drop across 7μF capacitor is 6V. Then
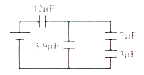
View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?

View SolutionTwo capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
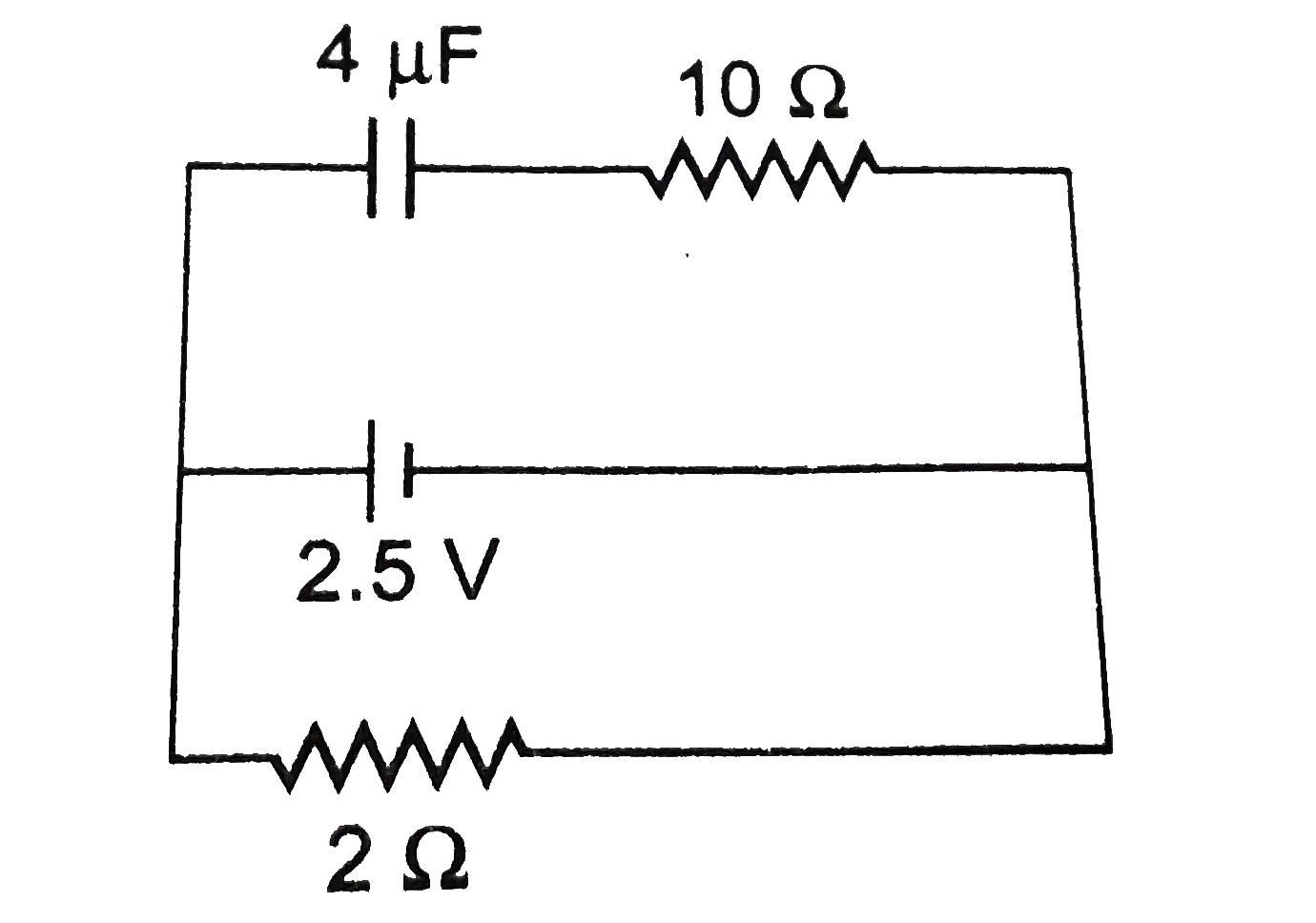
View SolutionA capacitor of 4μF is connected as shwon in the figure. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View Solution
